# Summary
残差链接。就和公司干活一样,层层总结容易失真,必要时可以跨级了解情况
## 1 一句话先说明白
> **残差 = “原样保留 + 微调”**
> 在 Transformer 里,每经过一次“注意力”或“前馈”处理,都会把**原始输入直接抄一份**并与处理后的结果相加,然后再做归一化。这样既能把新学到的东西叠加进来,又保证最初的关键信息和梯度不会在深层网络里被“稀释”或“爆炸”。
---
# 2 为什么需要这条“抄近路”?
|问题|如果没有残差会怎样|残差怎么帮忙|
|---|---|---|
|**梯度消失 / 爆炸**深度模型反向传播时,梯度在层与层之间不断相乘,容易过小或过大|网络越深越难训练,常常到几十层就“学不动”了|直接把输入 `x` 原封不动送到下一层,梯度至少能沿着这条 **恒等通道** 顺利传播|
|**学习效率低**每层都得从头学“我要输出什么”|如果本来就该保留大部分信息,网络却要重算一遍|只需学习 **差值 F(x) = 需要改动的那一点点**;“保持原样”= 把 F(x) 学成 0 很容易|
|**信息被过度加工**低层的词序、位置等细节后来用不上|细节在不断的矩阵乘法中被“搅烂”|残差像“高速公路应急车道”,让原始信号一路畅通留到高层随时取用|
|**深层网络退化**层数越多反而效果下降|每多一层都可能带来负面扰动|如果这一层真没帮助,网络可以让 F(x)≈0,整体就近似“跳过”|
---
# 3 用生活比喻快速感受
|场景|对应残差思想|
|---|---|
|**写论文改稿**:先把初稿整段复制,然后在旁边用批注“增删一句”|把输入原样复制 (`+x`),模型只写批注 (`F(x)`)|
|**导航**:高速路 + 匝道。主线保证你一直向前,匝道只在需要时绕出去改道|恒等通道传主干信息,子层 `F(x)` 负责“绕出去处理”|
|**做菜**:基底高汤先倒一锅,再慢慢调味|基底 `x` 不变,`F(x)` 添香料|
---
# 4 数学视角(很容易看懂)
1. **公式**
Output=LayerNorm(x+F(x; θ))\text{Output} = \mathrm{LayerNorm}(x + F(x;\,\theta))
- 这里 `x` 是输入,
- `F` 可以是“多头注意力”也可以是“前馈网络”,
- `θ` 是这一层要学的权重。
如果最优解就是“别动”,让 `F` 学成全 0 即可——梯度对 `θ` 会自动收敛到 0,训练很稳。
2. **梯度直通**
反向传播时
∂ Loss∂x = ∂ Loss∂(x+F) ⋅ 1⏟来自恒等支路 + ∂ Loss∂(x+F) ⋅ ∂F∂x⏟来自子层\frac{\partial\,\text{Loss}}{\partial x} \;=\; \underbrace{\frac{\partial\,\text{Loss}}{\partial (x+F)}\,⋅\,1}_{\text{来自恒等支路}} \;+\; \underbrace{\frac{\partial\,\text{Loss}}{\partial (x+F)}\,⋅\,\frac{\partial F}{\partial x}}_{\text{来自子层}}
“+1” 这一项确保即使 `∂F/∂x` 很小(梯度快消失),也还有一条路把信号传回来。
---
# 5 在 Transformer 里具体放哪?
一个 **Encoder 或 Decoder Layer** 有两个残差块(有时叫“子层”):
```text
┌───────────┐
x ──►[1]─►│Multi‑Head │
│ Attention│
└───────────┘
Add + Norm ←── 残差#1
│
▼
┌───────────┐
│Feed‑Forward│
└───────────┘
Add + Norm ←── 残差#2
│
▼ (送到下一层)
```
- **残差#1**:把做完注意力的结果与原始 `x` 相加;
- **残差#2**:把前馈结果与残差#1 的输出相加。
- Decoder 里还有第三个(跨注意力)残差,布局相同。
> **小细节:Pre-LN vs. Post-LN**
>
> - **Post‑LN(论文原版)**:Add‑Norm 在子层后;训练深层时容易不稳。
>
> - **Pre‑LN(现在更常见)**:先 LayerNorm,再做子层,再加残差;梯度更平滑,易于 48 层以上超深模型。
>
---
# 6 再回答 3 个常见“WHY”
1. **为什么不用门控 (Highway) 或 DenseNet 式拼接?**
- 门控要多学一套 σ/门参数;DenseNet 会让维度激增。
- 对 NLP 序列,简单加法足够稳、便宜、效果好。
2. **残差会不会让模型只学到“复制”?**
- 训练初期是这样(快速找到 Identity),随后梯度会推动 `F(x)` 捕捉真正有用的差异;否则损失不会下降。
3. **残差与“层叠自注意力”有什么关系?**
- 注意力更像 **加工厂**,残差像 **传送带**:保证货物原样走到底,同时允许中途加工升级。
---
## 7 60 字小结
> **残差连接 = 恒等快车道 + 可学习旁路**。
> 它让信息和梯度在几十层 Transformer 中无阻塞直达,高效避免退化与梯度消失,同时把“学会新知识”简化为“在旧基础上微调”,因此成为现代大模型不可或缺的基本构件。
>
>
> # Cues
# Notes
- [一、背景](#%E4%B8%80%E3%80%81%E8%83%8C%E6%99%AF)
- [1.1 梯度消失/爆炸](#1.1%20%E6%A2%AF%E5%BA%A6%E6%B6%88%E5%A4%B1/%E7%88%86%E7%82%B8)
- [1.2 网络退化(Degradation)](#1.2%20%E7%BD%91%E7%BB%9C%E9%80%80%E5%8C%96(Degradation))
- [二、思路](#%E4%BA%8C%E3%80%81%E6%80%9D%E8%B7%AF)
- [2.1 为什么需要更深的网络](#2.1%20%E4%B8%BA%E4%BB%80%E4%B9%88%E9%9C%80%E8%A6%81%E6%9B%B4%E6%B7%B1%E7%9A%84%E7%BD%91%E7%BB%9C)
- [2.2 理想中的深网络表现](#2.2%20%E7%90%86%E6%83%B3%E4%B8%AD%E7%9A%84%E6%B7%B1%E7%BD%91%E7%BB%9C%E8%A1%A8%E7%8E%B0)
- [三、实践和实验效果](#%E4%B8%89%E3%80%81%E5%AE%9E%E8%B7%B5%E5%92%8C%E5%AE%9E%E9%AA%8C%E6%95%88%E6%9E%9C)
- [3.1 构造恒等映射:残差学习(residule learning)](#3.1%20%E6%9E%84%E9%80%A0%E6%81%92%E7%AD%89%E6%98%A0%E5%B0%84%EF%BC%9A%E6%AE%8B%E5%B7%AE%E5%AD%A6%E4%B9%A0%EF%BC%88residule%20learning%EF%BC%89)
在Transformer中,数据过Attention层和FFN层后,都会经过一个**Add & Norm**处理。其中,Add为**residule block(残差模块)**,数据在这里进行**residule connection([残差连接](https://zhida.zhihu.com/search?content_id=190144936&content_type=Article&match_order=1&q=%E6%AE%8B%E5%B7%AE%E8%BF%9E%E6%8E%A5&zhida_source=entity))**。残差连接的思想最经典的代表就是2015年被提出的[[ResNet]]这个用于解决深层网络训练问题的模型最早被用于图像任务处理上,现在已经成为一种普适性的深度学习方法。这篇笔记将对此进行解析,笔记内容包括:
## 一、背景
在进行**深层**网络学习的过程中,有两个避不开的问题:
### 1.1 梯度消失/爆炸
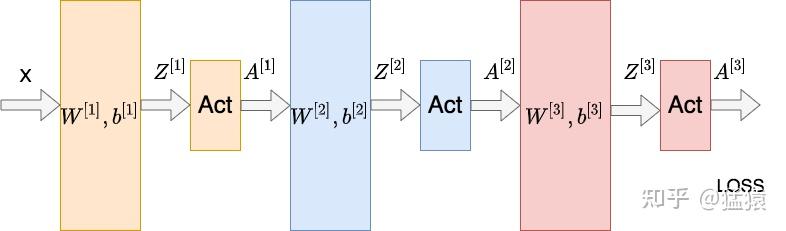
如图所示的三层神经网络,每一层的线性层和非线性层可以表示为:
$
\begin{aligned} Z^{[L]} &= W^{[L]} * A^{[L-1]} + b^{[L]} (线性变化层)\\ A^{[L]} &= g^{[L]}(Z^{[L]})(非线性变化/激活函数层) \end{aligned}
$
假设现在要计算第一层 $W^{[1]}$ 的梯度,那么根据链式法则,有:
$
\begin{aligned} \frac{\partial LOSS}{\partial W^{[1]}} & = \frac{\partial LOSS}{\partial A^{[3]}}\frac{\partial A^{[3]}}{\partial Z^{[3]}}\frac{\partial Z^{[3]}}{\partial A^{[2]}}\frac{\partial A^{[2]}}{\partial Z^{[2]}}\frac{\partial Z^{[2]}}{\partial A^{[1]}}\frac{\partial A^{[1]}}{\partial Z^{[1]}}\frac{\partial Z^{[1]}}{\partial W^{[1]}}\\ & = \frac{\partial LOSS}{\partial A^{[3]}}{g^{[3]}}'W^{[3]}{g^{[2]}}'W^{[2]}{g^{[1]}}'\frac{\partial Z^{[1]}}{\partial W^{[1]}} \end{aligned}
$
如果在神经网络中,多层都满足 ${g^{[L]}}'W^{[L]} > 1$,则越往下的网络层的梯度越大,这就造成了**梯度爆炸**的问题。反之,若多层都满足 ${g^{[L]}}'W^{[L]} < 1$,则越往下的网络层梯度越小,引起**梯度消失**的问题。而在深度学习网络中,为了让模型学到更多非线性的特征,在激活层往往使用例如**sigmoid**这样的激活函数。对sigmoid来说,**其导数的取值范围在** $(0,\frac{1}{4}]$,在层数堆叠的情况下,更容易出现梯度消失的问题。
面对[梯度爆炸](梯度爆炸.md)消失/爆炸的情况,可以通过Normalization等方式解决,使得模型最终能够收敛。
### 1.2 网络退化(Degradation)
因为梯度消失/爆炸所导致的深层网络模型不收敛的问题,已经得到了解决。那么现在新的问题出现了:在模型能够收敛的情况下,网络越深,模型的准确率越低,同时,模型的准确率先达到饱和,此后迅速下降。这个情况我们称之为网络退化(Degradation)。如下图,56层网络在测试集(右)上的错误率比20层网络要更高,这个现象也不是因为overfitting所引起的,因为在训练集上,深层网络的表现依然更差。
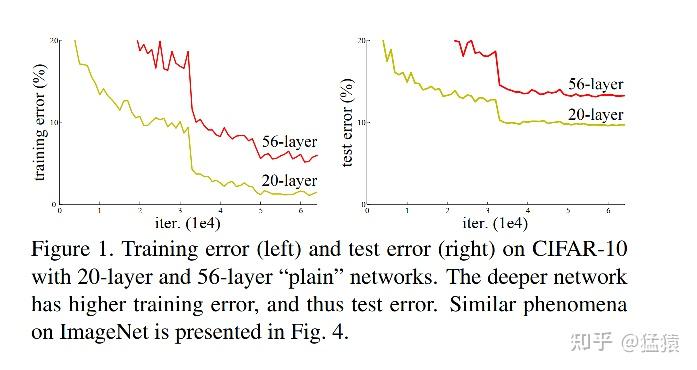
因此,<u>ResNet就作为一种解决网络退化问题的有效办法出现了</u>,借助ResNet,我们能够有效训练出更深的网络模型(可以超过1000层),使得深网络的表现不差于浅网络。
## 二、思路
### 2.1 为什么需要更深的网络
神经网络帮我们避免了繁重的特征工程过程。借助神经网络中的非线形操作,可以帮助我们更好地拟合模型的特征。为了增加模型的表达能力,一种直觉的想法是,增加网络的深度,一来使得网络的每一层都尽量学到不同的模式,二来更好地利用网络的非线性拟合能力。
### 2.2 理想中的深网络表现
理想中的深网络,其表现不应该差于浅网络。举一个简单的例子,下图左边是2层的浅网络,右边是4层的深网络,我们只要令深网络的最后两层的输入输出相等,那么两个网络就是等效的,这种操作被称为**恒等映射(Identity Mapping)。**
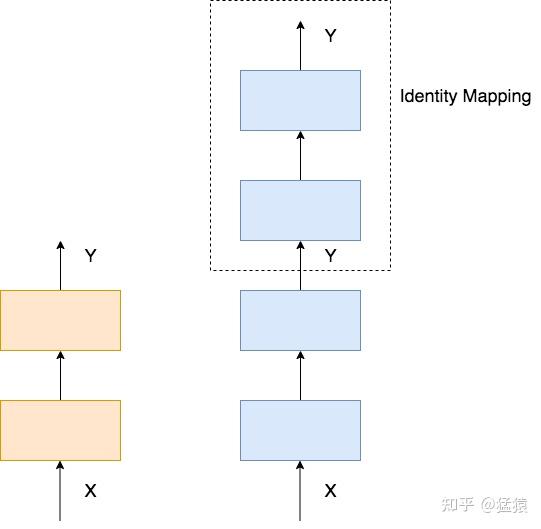
当然,这样完全相等的映射是一种极端情况,更为理想的情况是,在网络的深层,让网络尽量逼近这样的极端情况,使得网络在学到新东西的同时,其输出又能逼近输入,这样就能保证深网络的效果不会比浅网络更差。
**总结:在网络的深层,需要学习一种恒等映射(Identity Mapping)。**
## 三、实践和实验效果
### 3.1 构造恒等映射:残差学习(residule learning)
最暴力的构造恒等映射的方法,就是在相应网络部分的尾端增加一层学习层 $W^{[IM]}$,来满足输出和输入逼近。但是本来深网络要学的参数就很庞大了,再构造新的参数层,又增加了模型的复杂度。
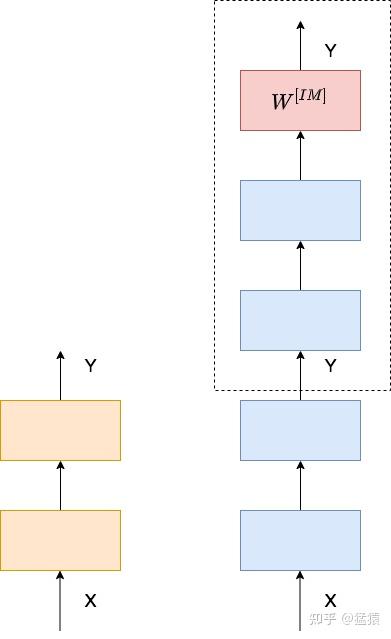
能不能在不添加参数层的情况下,实现恒等映射的功能?考虑下图:
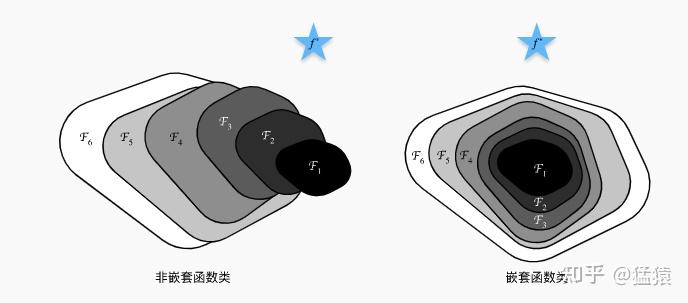
蓝色星星 $\mathcal{f}^*$ 是“真正”拟合我们数据集的函数,而 $\mathcal{F}_1,...,\mathcal{F}_6$ 表示分别表示不同层数的神经网络(层数为1的,层数为2的...)。在左边的构造方式中,函数是非嵌套的,可以发现6层神经网络可能比单层神经网络距离最优解更远。而在右边的嵌套式构造中,则保证了更多层的神经网络至少能取到更浅的神经网络的最优解。受到这一思想的启发,我们在深层网络中引入残差模块,具体运作方式如下:
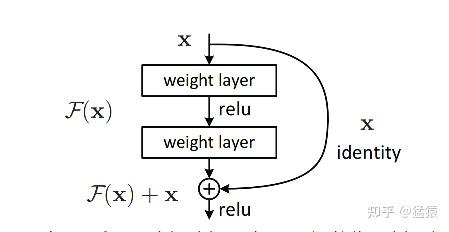
如图所示,这个残差模块包含了神经网络中的两层,其中,$X$ 表示输入,$\mathcal{F}(X)$ 表示过这两层之后的结果,$\mathcal{H}(X)$ 表示恒等映射,则在这样的构造方式下,恒等映射可以写成:$\mathcal{H}(X) = \mathcal{F}(X) + X$(1)
$\mathcal{F}(X)$ 就被称之为**残差函数(residule function)。**在网络深层的时候,在优化目标的约束下,模型通过学习使得 $\mathcal{F}(X)$ 逼近0**(residule learning)**,让深层函数在学到东西的情况下,又不会发生网络退化的问题。
通过这样的构造方式,让 $\mathcal{F}(X)$ 嵌套在了 $\mathcal{H}(X)$ 中,这样跃层构造的方式也被称为**残差连接(residule connection)/ 跳跃连接(skip connection)/短路(shortcuts)**。模型并不是严格的跨越2层,可以根据需要跨越3,4层进行连接。同时,等式(1)是在假设输入输出同维,即 $\mathcal{F}(X)$ 和 $X$ 同维的情况,不同维时,只需要在 $X$ 前面增加一个转换矩阵 $W_{s}$ 即可。
### 3.2 实验过程及结果
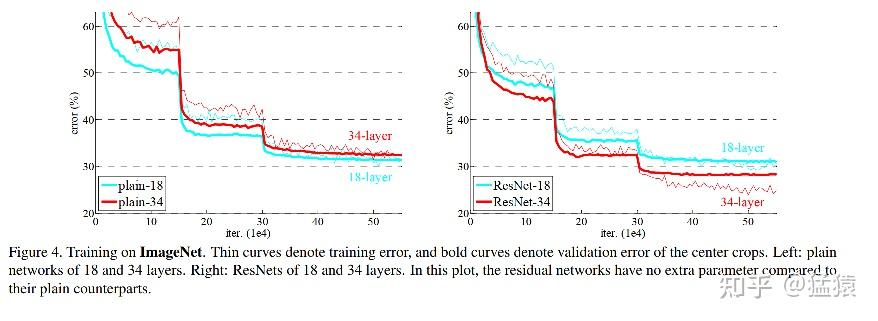
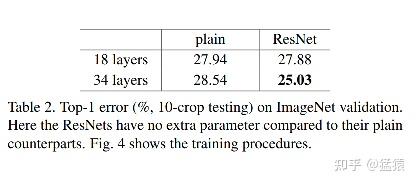
在ResNet的论文中,做了很丰富的实验,这里仅贴出它在ImageNet 2012数据集上的试验结果。这个实验的网络以VGG网络为参考,构造了**34-layer plain DNN**和**34-layer residule DNN。**前者是一个标准的深层网络,后者是增加残差处理的深层网络。基本构造如下:(图很小吧,都怪网络太深,没关系,不看也可以)
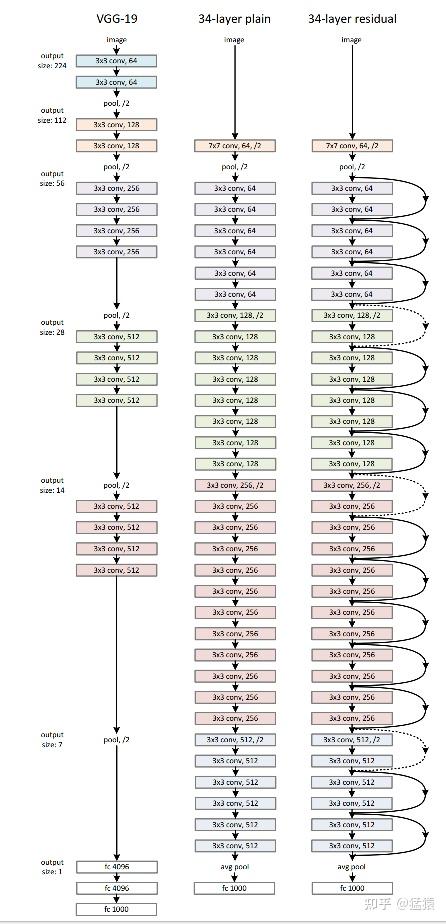
以下是实验结果。左图是18层和34层的plain DNN,右是18层和34层的residule DNN。粗线表示训练集上的错误率,细线表示验证集上的错误率。可以发现在残差网络中,深网络的错误率都已经被压到了浅网络之下,同时也比plain DNN的错误率更低。
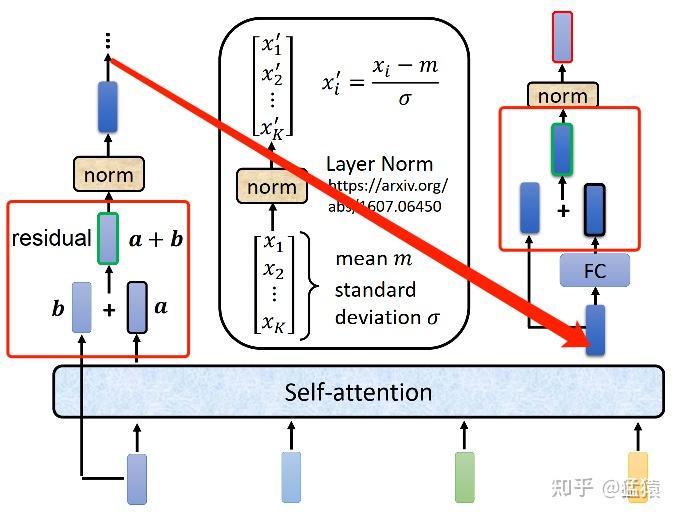
## 四、Transformer中的残差连接
在transformer的encoder和decoder中,各用到了6层的attention模块,每一个attention模块又和一个FeedForward层(简称FFN)相接。对每一层的attention和FFN,都采用了一次残差连接,即把每一个位置的输入数据和输出数据相加,使得Transformer能够有效训练更深的网络。在残差连接过后,再采取Layer Nomalization的方式。具体的操作过程见下图,箭头表示画不下了,从左边转到右边去画: