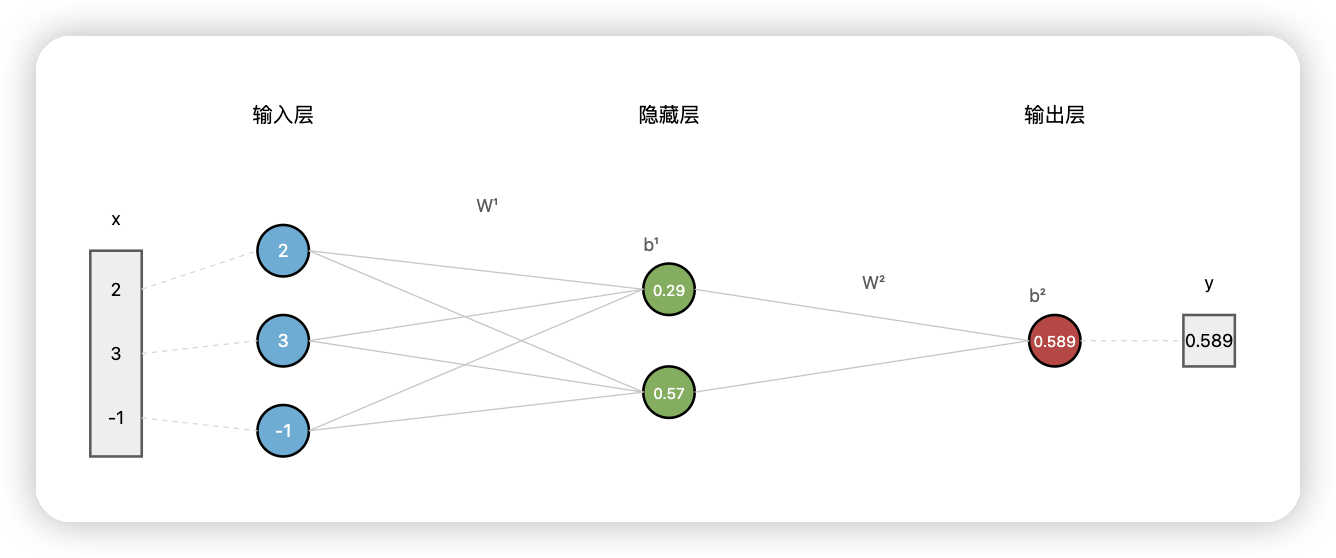
# Summary 本教程完整展示了一个两层神经网络的前向传播和反向传播过程，包括： 1. **前向传播**：逐层计算激活值 2. **损失计算**：使用均方误差 3. **[反向传播](反向传播.md)**：从输出层向输入层计算梯度 *每个 W 矩阵里的每个位置下次变化的 unit* 4. **参数更新**：使用梯度下降法 5. **验证效果**：损失值降低 # Cues # Notes ## 网络结构  ### 网络参数初始化 **输入层到隐藏层：** - 权重矩阵：$W^{(1)} = \begin{bmatrix} 0.2 & -0.5 & 0.1 \ -0.3 & 0.4 & 0.2 \end{bmatrix}$ - 偏置向量：$b^{(1)} = \begin{bmatrix} 0.3 \ -0.1 \end{bmatrix}$ **隐藏层到输出层：** - 权重矩阵：$W^{(2)} = \begin{bmatrix} 0.5 & 0.2 \end{bmatrix}$ - 偏置：$b^{(2)} = 0.1$ **输入数据：** - $x = \begin{bmatrix} 2 \ 3 \ -1 \end{bmatrix}$ - 目标值：$y = 1$ ## 一、前向传播 ### 1. 输入层到隐藏层的计算 **公式：** $z^{(1)} = W^{(1)}x + b^{(1)}$ $a^{(1)} = \sigma(z^{(1)})$ **矩阵计算：** $z^{(1)} = \begin{bmatrix} 0.2 & -0.5 & 0.1 \ -0.3 & 0.4 & 0.2 \end{bmatrix} \begin{bmatrix} 2 \ 3 \ -1 \end{bmatrix} + \begin{bmatrix} 0.3 \ -0.1 \end{bmatrix}$ **详细展开：** $\begin{align} z_1^{(1)} &= 0.2 \times 2 + (-0.5) \times 3 + 0.1 \times (-1) + 0.3 \ &= 0.4 - 1.5 - 0.1 + 0.3 = -0.9 \end{align}$ $\begin{align} z_2^{(1)} &= (-0.3) \times 2 + 0.4 \times 3 + 0.2 \times (-1) + (-0.1) \ &= -0.6 + 1.2 - 0.2 - 0.1 = 0.3 \end{align}$ **结果：** $z^{(1)} = \begin{bmatrix} -0.9 \ 0.3 \end{bmatrix}$ **激活函数：** $a^{(1)} = \sigma(z^{(1)}) = \begin{bmatrix} \sigma(-0.9) \ \sigma(0.3) \end{bmatrix} = \begin{bmatrix} \frac{1}{1 + e^{0.9}} \ \frac{1}{1 + e^{-0.3}} \end{bmatrix} = \begin{bmatrix} 0.289 \ 0.574 \end{bmatrix}$ ### 2. 隐藏层到输出层的计算 **公式：** $z^{(2)} = W^{(2)}a^{(1)} + b^{(2)}$ $a^{(2)} = \sigma(z^{(2)})$ **矩阵计算：** $z^{(2)} = \begin{bmatrix} 0.5 & 0.2 \end{bmatrix} \begin{bmatrix} 0.289 \ 0.574 \end{bmatrix} + 0.1$ **详细展开：** $\begin{align} z^{(2)} &= 0.5 \times 0.289 + 0.2 \times 0.574 + 0.1 \ &= 0.1445 + 0.1148 + 0.1 = 0.3593 \end{align}$ **激活函数：** $a^{(2)} = \sigma(0.3593) = \frac{1}{1 + e^{-0.3593}} = 0.589$ ## 二、[[损失函数]]计算 **均方误差(MSE)：** $C_0 = (a^{(2)} - y)^2 = (0.589 - 1)^2 = (-0.411)^2 = 0.169$ ## 三、反向传播 ### 1. 计算输出层的误差信号 **定义误差信号：** $\delta^{(2)} = \frac{\partial C_0}{\partial z^{(2)}}$ **链式法则展开：** $\delta^{(2)} = \frac{\partial C_0}{\partial a^{(2)}} \cdot \frac{\partial a^{(2)}}{\partial z^{(2)}}$ **各项计算：** - $\frac{\partial C_0}{\partial a^{(2)}} = 2(a^{(2)} - y) = 2(0.589 - 1) = -0.822$ - $\frac{\partial a^{(2)}}{\partial z^{(2)}} = \sigma'(z^{(2)}) = a^{(2)}(1 - a^{(2)}) = 0.589 \times 0.411 = 0.242$ **结果：** $\delta^{(2)} = -0.822 \times 0.242 = -0.199$ ### 2. 计算输出层参数的梯度 **权重梯度公式：** $\frac{\partial C_0}{\partial W^{(2)}} = \delta^{(2)} \cdot (a^{(1)})^T$ **矩阵计算：** $\frac{\partial C_0}{\partial W^{(2)}} = -0.199 \times \begin{bmatrix} 0.289 & 0.574 \end{bmatrix} = \begin{bmatrix} -0.0575 & -0.1142 \end{bmatrix}$ **偏置梯度公式：** $\frac{\partial C_0}{\partial b^{(2)}} = \delta^{(2)} = -0.199$ ### 3. 计算隐藏层的误差信号 **公式：** $\delta^{(1)} = (W^{(2)})^T \delta^{(2)} \odot \sigma'(z^{(1)})$ **步骤分解：** **第一步：计算反向传播的误差** $(W^{(2)})^T \delta^{(2)} = \begin{bmatrix} 0.5 \ 0.2 \end{bmatrix} \times (-0.199) = \begin{bmatrix} -0.0995 \ -0.0398 \end{bmatrix}$ **第二步：计算激活函数导数** $\sigma'(z^{(1)}) = a^{(1)} \odot (1 - a^{(1)}) = \begin{bmatrix} 0.289 \ 0.574 \end{bmatrix} \odot \begin{bmatrix} 0.711 \ 0.426 \end{bmatrix} = \begin{bmatrix} 0.2055 \ 0.2445 \end{bmatrix}$ **第三步：Hadamard积** $\delta^{(1)} = \begin{bmatrix} -0.0995 \ -0.0398 \end{bmatrix} \odot \begin{bmatrix} 0.2055 \ 0.2445 \end{bmatrix} = \begin{bmatrix} -0.0204 \ -0.0097 \end{bmatrix}$ ### 4. 计算隐藏层参数的梯度 **权重梯度公式：** $\frac{\partial C_0}{\partial W^{(1)}} = \delta^{(1)} \cdot x^T$ **矩阵计算：** $\frac{\partial C_0}{\partial W^{(1)}} = \begin{bmatrix} -0.0204 \ -0.0097 \end{bmatrix} \times \begin{bmatrix} 2 & 3 & -1 \end{bmatrix} = \begin{bmatrix} -0.0408 & -0.0612 & 0.0204 \ -0.0194 & -0.0291 & 0.0097 \end{bmatrix}$ **偏置梯度公式：** $\frac{\partial C_0}{\partial b^{(1)}} = \delta^{(1)} = \begin{bmatrix} -0.0204 \ -0.0097 \end{bmatrix}$ ## 四、参数更新 **学习率：** $\eta = 0.1$ **更新公式：** $\theta_{new} = \theta_{old} - \eta \cdot \frac{\partial C_0}{\partial \theta}$ ### 输出层参数更新 **权重更新：** $W^{(2)}_{new} = \begin{bmatrix} 0.5 & 0.2 \end{bmatrix} - 0.1 \times \begin{bmatrix} -0.0575 & -0.1142 \end{bmatrix} = \begin{bmatrix} 0.5058 & 0.2114 \end{bmatrix}$ **偏置更新：** $b^{(2)}_{new} = 0.1 - 0.1 \times (-0.199) = 0.1199$ ### 隐藏层参数更新 **权重更新：** $W^{(1)}_{new} = \begin{bmatrix} 0.2 & -0.5 & 0.1 \ -0.3 & 0.4 & 0.2 \end{bmatrix} - 0.1 \times \begin{bmatrix} -0.0408 & -0.0612 & 0.0204 \ -0.0194 & -0.0291 & 0.0097 \end{bmatrix}$ $W^{(1)}_{new} = \begin{bmatrix} 0.2041 & -0.4939 & 0.0980 \ -0.2981 & 0.4029 & 0.1990 \end{bmatrix}$ **偏置更新：** $b^{(1)}_{new} = \begin{bmatrix} 0.3 \ -0.1 \end{bmatrix} - 0.1 \times \begin{bmatrix} -0.0204 \ -0.0097 \end{bmatrix} = \begin{bmatrix} 0.3020 \ -0.0990 \end{bmatrix}$ ## 五、验证：使用更新后的参数进行前向传播 ### 隐藏层计算（使用更新后的参数） $z^{(1)}_{new} = W^{(1)}_{new} \cdot x + b^{(1)}_{new}$ $a^{(1)}_{new} = \sigma(z^{(1)}_{new})$ ### 输出层计算（使用更新后的参数） $z^{(2)}_{new} = W^{(2)}_{new} \cdot a^{(1)}_{new} + b^{(2)}_{new}$ $a^{(2)}_{new} = \sigma(z^{(2)}_{new}) \approx 0.595$ ### 新的损失值 $C_{new} = (0.595 - 1)^2 = 0.164$ **改进效果：** - 原损失值：$C_{old} = 0.169$ - 新损失值：$C_{new} = 0.164$ - 损失减少：$\Delta C = 0.005$ ## 六、训练流程图 ```mermaid flowchart TD A[初始化参数] --> B[前向传播] B --> C[计算损失 C₀] C --> D[计算输出层误差 δ²] D --> E[计算输出层梯度] E --> F[反向传播误差到隐藏层] F --> G[计算隐藏层梯度] G --> H[更新所有参数] H --> I{检查停止条件} I -->|继续| B I -->|停止| J[训练完成] style A fill:#d0f4de style J fill:#f4d0d0 style I fill:#f4e5d0 ```