#第一性原理 逻辑回归可以看作是没有隐藏层的[[神经网络]]，即单层感知机，哈哈，而多层感知机通过引入隐藏层和非线性激活，极大地提升了模型的表达能力，可以解决更复杂的分类（或回归）问题。 如果我们想要得到一个概率而不是简单的0或1，那么我们可以用[逻辑回归 1](逻辑回归%201.md) # 1. 模型假设 对于输入特征向量 $\mathbf{x}$ 和参数向量 $\boldsymbol{\theta}$（也可以记作 $w$），逻辑回归先计算线性组合： $z = \boldsymbol{\theta}^T \mathbf{x}.$ 然后通过**sigmoid 函数**将 $z$ 映射到 (0,1) 区间，作为概率输出： $h_\theta(x) = \sigma(z) = \frac{1}{1+e^{-z}}.$ 这里 $h_\theta(x)$ 表示样本属于正类（比如标签为1）的概率。 --- # 2. 损失函数（[[交叉熵 cross_entropy]]） 由于输出是概率，所以逻辑回归使用的是**对数损失函数（Log Loss，也叫交叉熵损失）**。对于单个样本，其损失可以表示为： $J(\theta) = -\Bigl[y \log(h_\theta(x)) + (1-y) \log(1-h_\theta(x))\Bigr],$ 其中： - $y$ 是真实标签（0 或 1）， - $h_\theta(x)$ 是预测的概率。 对于整个训练集（共有 $m$ 个样本），平均损失为： $J(\theta) = -\frac{1}{m} \sum_{i=1}^{m} \Bigl[y^{(i)} \log(h_\theta(x^{(i)})) + (1-y^{(i)}) \log(1-h_\theta(x^{(i)}))\Bigr].$ --- # 3. 参数优化 和线性回归类似，我们的目标是调整参数 $\boldsymbol{\theta}$ 使得损失函数 $J(\theta)$ 达到最小。常见的方法有梯度下降： 1. **计算梯度**：对 $\theta_j$ 求偏导 $\frac{\partial J(\theta)}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^{m} \left(h_\theta(x^{(i)}) - y^{(i)}\right)x_j^{(i)}.$ 2. **更新参数**： $\theta_j:= \theta_j - \alpha \frac{\partial J(\theta)}{\partial \theta_j},$ 其中 $\alpha$ 是学习率。 通过不断迭代这个过程，就可以找到使得 $J(\theta)$ 最小的参数。 --- # 4. 总结 - **模型输出**：逻辑回归利用 sigmoid 函数将线性组合结果映射到 (0,1)，输出一个概率。 - **损失函数**：采用交叉熵损失（对数损失）来衡量预测概率与真实标签之间的差异。 - **参数优化**：通过梯度下降（或其他优化方法）不断调整参数 $\boldsymbol{\theta}$，直到损失函数最小。 这种方式使得逻辑回归在二分类问题中非常有效，也可以扩展到多分类问题（如使用 softmax 函数）。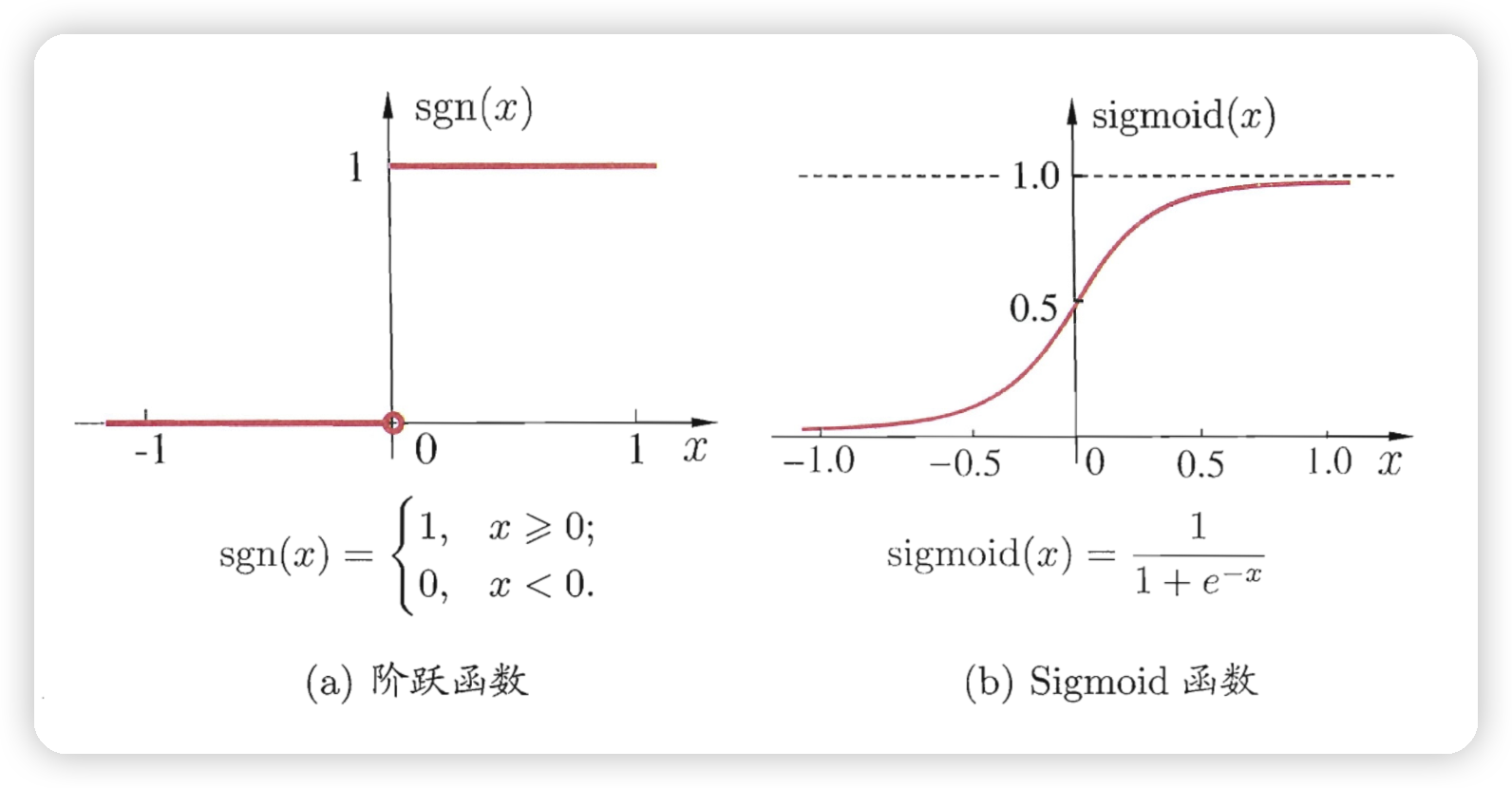 # 逻辑回归 如果我们想要得到一个概率而不是简单的0或1，那么我们可以用[逻辑回归](逻辑回归.md)，其与感知机的区别是  用了 Sigmoid 函数来把结果映射为概率，而感知机只是用阶跃函数把结果映射为 0 和 1