# 💡 Summary **蒙特卡洛（Monte Carlo）** 是欧洲一个著名的赌场（位于摩纳哥），以赌博闻名。 本质：用大量随机试验，估算难以直接计算的结果 ```python 【一句话理解】 用大量随机试验，估算难以直接计算的结果 【核心思想】 "算不出来？那就随机试一万次，看看结果！" 【形象比喻】 • 投飞镖估算π → 几何概率 • 钓鱼估算鱼数 → 抽样估计 • 赌场模拟 → 随机过程 【关键步骤】 1. 定义问题（要估算什么？） 2. 建立模型（随机变量是什么？） 3. 大量抽样（重复N次） 4. 统计汇总（平均、概率、分位数） 5. 评估精度（误差 ∝ 1/√N） 【适用场景】 ✓ 复杂问题（无解析解） ✓ 高维问题（很多变量） ✓ 随机过程（股价、排队...） ✓ 风险分析（概率分布） 【精度法则】 • N=100 → 误差 ~10% • N=10,000 → 误差 ~1% • N=1,000,000 → 误差 ~0.1% 精度翻倍，样本量要4倍！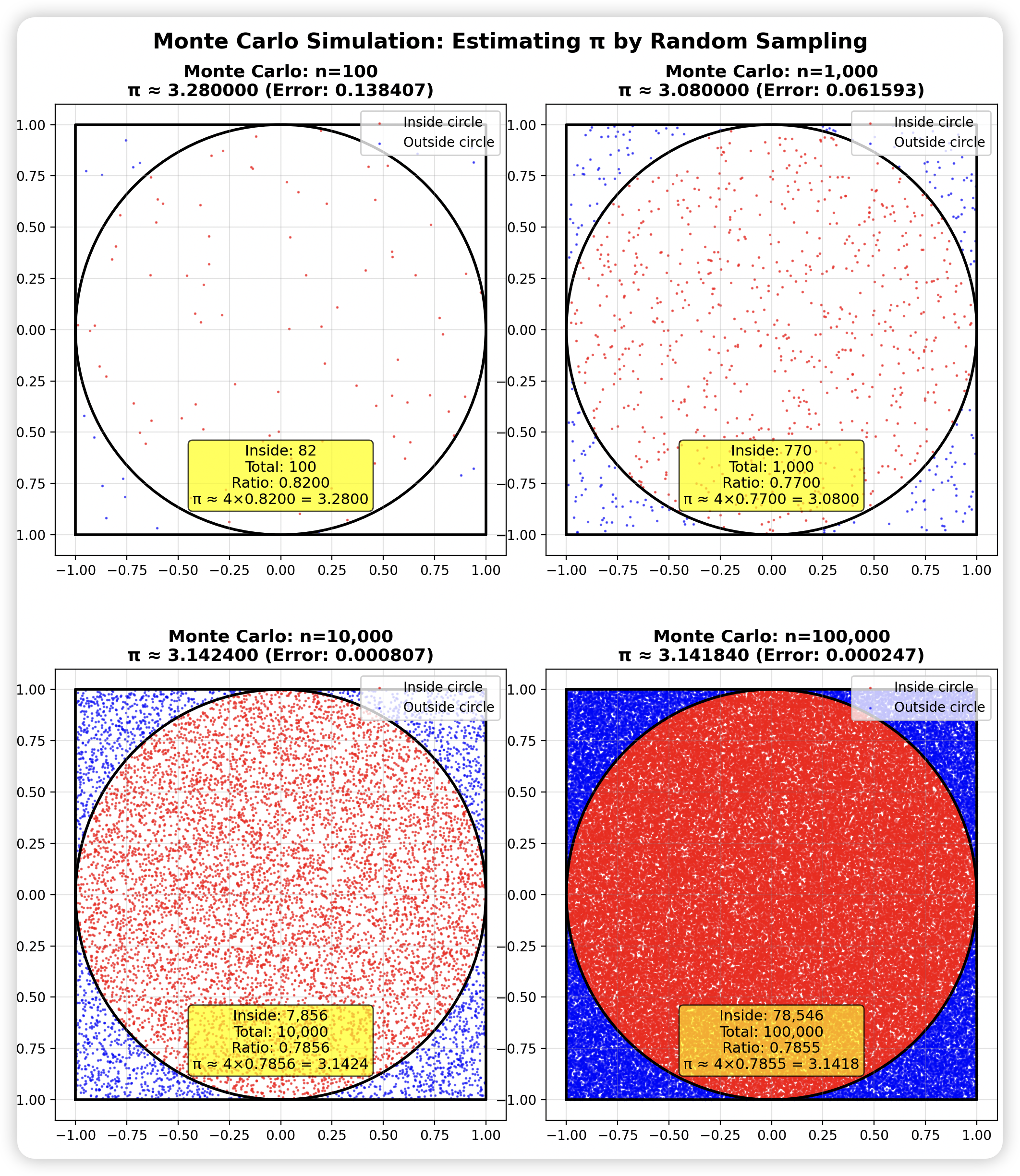 ``` 【实际应用】 • 金融：[[期权]]定价、风险管理 • 物理：粒子模拟、量子计算 • 统计：[[Bootstrap]]、贝叶斯推断 • 工程：可靠性分析、系统仿真 • AI：强化学习、[[蒙特卡洛树]]搜索 # 🧩 Cues # 🪞Notes 场景：投飞镖估算圆周率 π ```python print(" 1. 画一个正方形，里面画个圆") print(" 2. 随机投飞镖（比如10000次）") print(" 3. 统计落在圆内的比例") print(" 4. 圆面积/正方形面积 = π/4") print(" 5. 推算出 π") ```