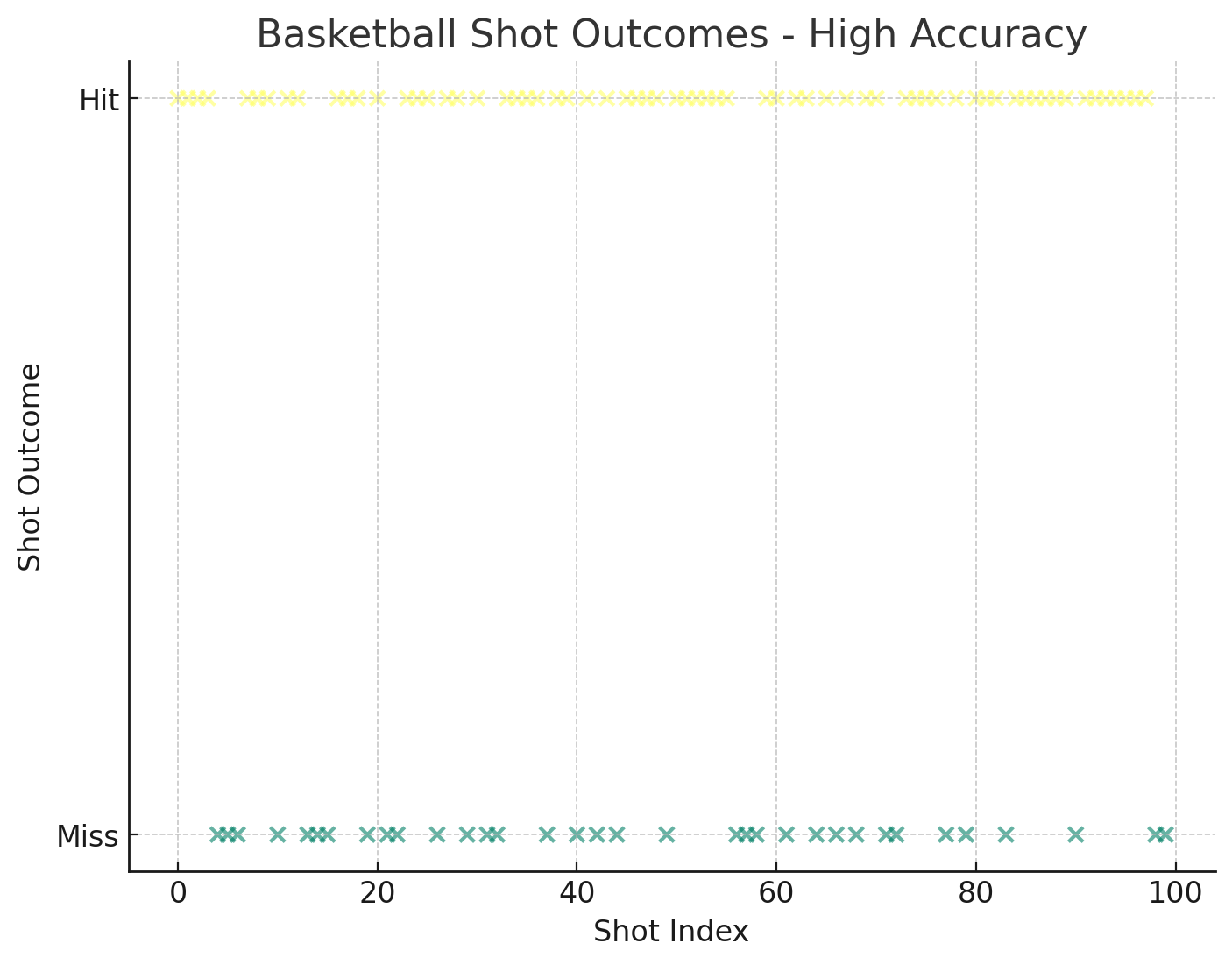
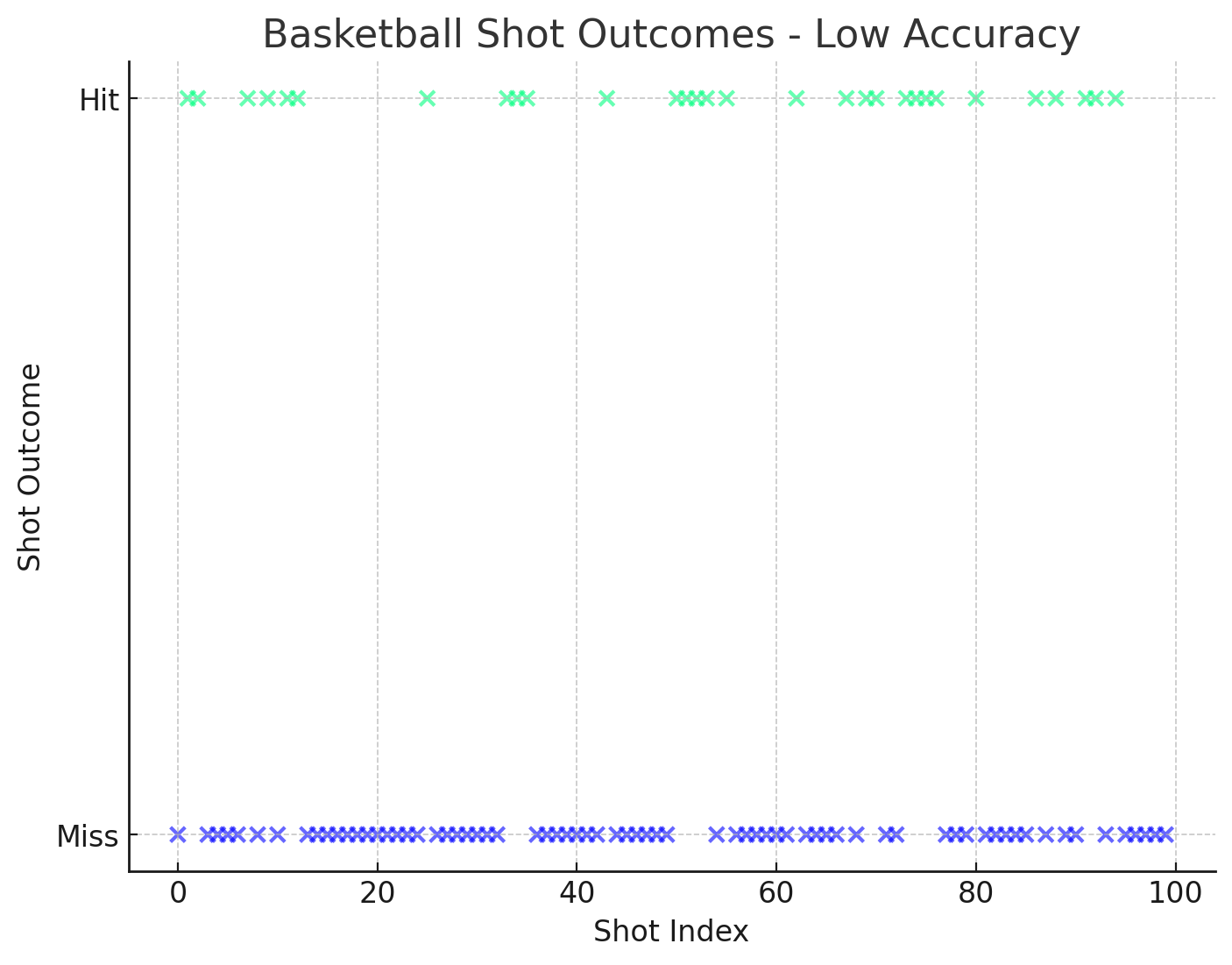
# Summary 某个场景即某种 hit 与 miss 之比出现的概率 # Cues # Notes ## 投篮场景  ### 投篮的散点图   横轴是样本序号 index，纵轴是观测到结果的话，散点图上应该只有两条横线，因为只有两种观测值，要么投篮投中，要么投篮不中， ### 投中的比投丢的 - 二项分布 本质上，我们好奇的是两根横线的长短之比，也就是中了几颗，不中几颗？所有的投中投丢比就构成了二项分布。二项分布的概率公式就可以帮助计算出某个场景即某种 hit 与 miss 之比出现的概率。