# Summary

为啥叫先验概率,因为 X 还没发生
```python
def bayes_update(prior, likelihood_h1, likelihood_h0):
"""
贝叶斯更新函数
prior: 假设1的先验概率
likelihood_h1: P(证据|假设1)
likelihood_h0: P(证据|假设0)
返回: 假设1的后验概率
"""
# 任务:实现贝叶斯更新
posterior = (prior * likelihood_h1) / (prior * likelihood_h1 + ((1 - prior) * likelihood_h0)) # 填写公式
return posterior
```
*用新证据更新旧信念。*
1. 先验概率,去到一个路边不正规赌场,小明和小王怀疑筛子有问题,分别认为有问题的概率是 0.1 和 0.3
2. [[似然函数]],真筛子出 6 的概率是 1/6,假筛子出 6 的概率是 1/2
3. 后验概率,随着他们去摇色子看到不同的结果,他们会不断更新自己的先验概率,比如一直是 6,两个人认为有问题的概率会快速飙升到 100%,一直是平均随机的,两个人认为有问题的概率会快速降到接近 0%
4. 贝叶斯因子,如果这个作弊筛子设计成偏向 6 的,那么 6 在摇的过程中的出现就会是一个正因子,增加两个人认为作弊的概率上涨
## 详细对应关系
| 文本分类概念 | 骰子场景对应 | 具体含义 | | |
| ----------------------------- | --------------------------------- | --------------- | --- | --- |
| **分类目标** | | | | |
| 作者(莎士比亚/马洛)| 骰子类型(公平/作弊)| 我们要判断的类别 | | |
| **观察证据** | | | | |
| 词频向量 | 掷骰序列 | 我们观察到的数据 | | |
| 单个词出现次数 | 某个点数出现次数 | 特征的具体值 | | |
| **概率成分** | | | | |
| $P(\text{作者})$ | $P(\text{骰子类型})$ | **先验概率** | | |
| = 作者的初始可能性 | = 0.8(公平)或 0.2(作弊)| 没看到证据前的信念 | | |
| $P(\text{词频} \mid \text{作者})$ | $P(\text{掷出结果} \mid \text{骰子类型})$ | **似然** | | |
| = 该作者使用这些词的概率 | = 该骰子掷出这些点数的概率 | 如果假设为真,看到证据的可能性 | | |
| $P(\text{作者} \mid \text{词频})$ | $P(\text{骰子类型} \mid \text{掷出结果})$ | **后验概率** | | |
| = 看到词频后的作者概率 | = 看到结果后的骰子类型概率 | 综合证据后的更新信念 | | |
# Cues
https://colab.research.google.com/drive/1JeLkzQRYywms9BwmQzaGtUdD51Tptle4#scrollTo=FoNWbDxbW31M
[贝叶斯主义者](贝叶斯主义者.md)
[凯利公式](凯利公式.md)
# Notes
## 贝叶斯公式
```python
def bayes_update(prior, likelihood_h1, likelihood_h0):
"""
贝叶斯更新函数
prior: 假设1的先验概率
likelihood_h1: P(证据|假设1)
likelihood_h0: P(证据|假设0)
返回: 假设1的后验概率
"""
# 任务:实现贝叶斯更新
posterior = (prior * likelihood_h1) / (prior * likelihood_h1 + ((1 - prior) * likelihood_h0)) # 填写公式
return posterior
```
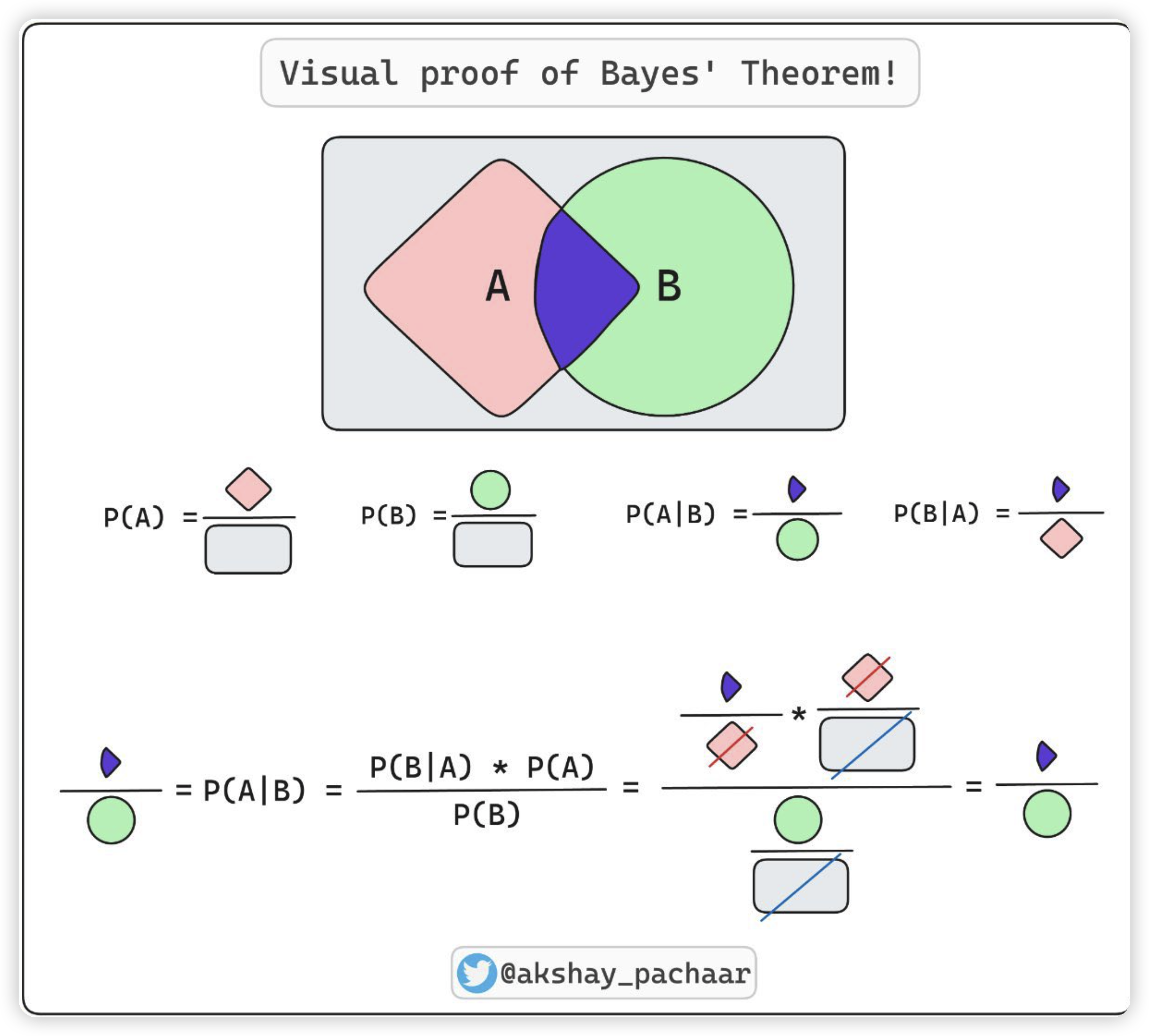
贝叶斯公式的核心是区分那两个符号一个是条件概率,另一个是同时发生. 一个是局部视角 一个是全局视角
| **概念** | **作用** |
|---|---|
| **贝叶斯定理** | 用已知数据计算某事件发生的概率 |
| **贝叶斯分类** | 用概率推理进行分类(如垃圾邮件检测)|
| **朴素贝叶斯** | 假设特征相互独立,简单高效 |
| **贝叶斯网络** | 允许特征之间有依赖关系,适用于更复杂的问题 |
贝叶斯分类的核心就是:**根据历史数据计算某个类别的概率,再用这个概率做出分类决策**。如果你想自己动手试试,我可以帮你写个 Python 代码来演示垃圾邮件分类,你感兴趣吗?