# Summary
Scaling Law 不是 AI 的专利, 而是所有"信息系统优化"的普遍规律:
场景:为什么 OpenAI 训练 GPT-3 时,选择用 **1750亿** 参数和 **3000亿** token 的数据,而不是用 **1万亿** 参数和 **100亿** token 的数据!
原因:他们找到了那个计算效率最高的“甜点”。找到固定算力([[FLOPs]])约束下,[[模型参数]]和数据量的最优配比
## 人类版 [[Scaling Law]]
[[学习@]]:学而不思则罔,思而不学则罔。
学习时间固定的情况下:
1. 时间分配:90 小时冥想训练大脑 + 10 小时做题 结果:智商暴涨,但只见过 50 道题 → 考试遇到新题型懵逼 ``` **对应**:GPT-3 (175B 参数 + 300B tokens) → 模型太大,数据太少,过拟合 ❌失败策略
2. 时间分配:5 小时思考学基础 + 95 小时疯狂刷题 结果:做了 10000 道题,但脑容量只记住了 100 个模式 → 大量重复劳动 ❌失败策略
| 深度学习 | 人类学习 | 本质 |
| ------------ | ---- | ------- |
| **计算预算 (C)** | 学习时间 | 总资源/能量 |
| **模型参数 (N)** | 思考能力 | 信息容器的大小 |
| **训练数据 (D)** | 学习材料 | 外部信息输入 |
Lab 3 的精髓在于:**不用自己造 GPU 集群,也能通过 API 和回归,把“大模型到底多大合算”这个问题搞清楚**。对于刚接触深度学习的后端同学,这既是一次理解 Transformer 能力极限的机会,也是一次把工程“实验指标 ➟ 数据库 ➟ 分析”流水线跑通的实战练习。祝你顺利完成!
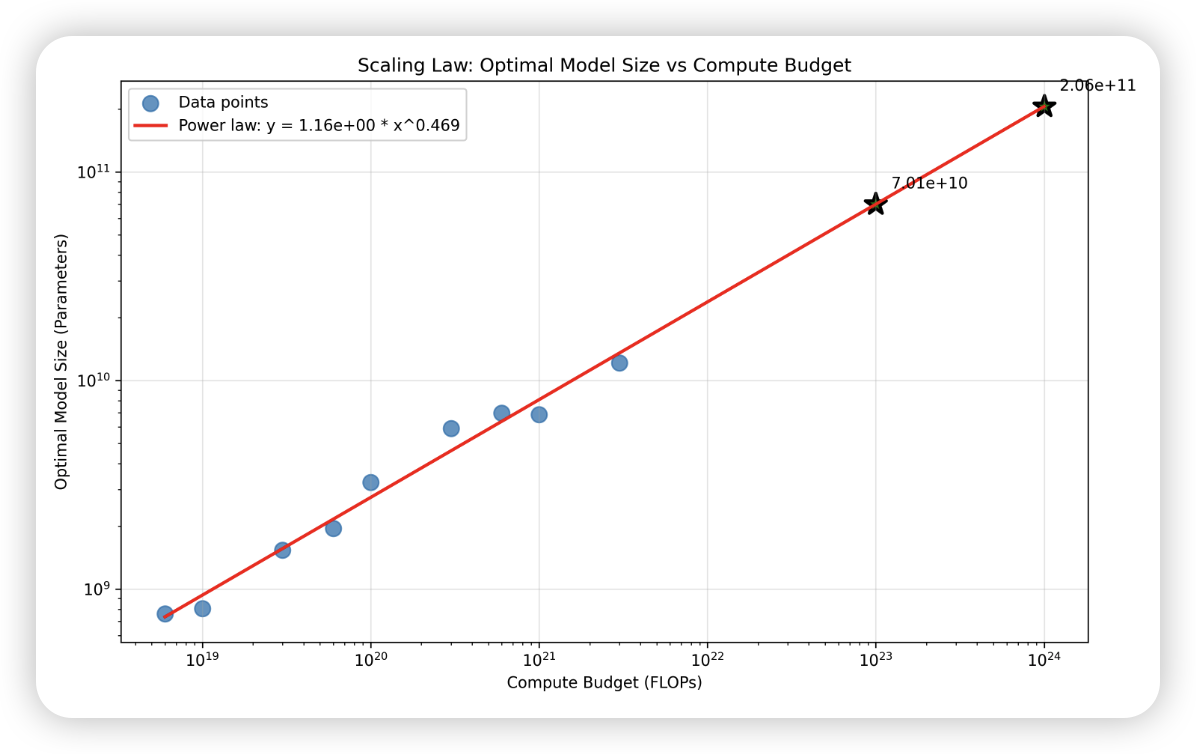
我们发现了一个惊人的规律:**最优参数量 (N) 正比于计算预算 (C) 的某个幂次方**。画在对数坐标系上,它就是一条直线!
得到了一个计算函数
```py
def plan_model_training(budget_flops):
# 根据缩放定律计算最优配置
optimal_params = 1.163 * (budget_flops ** 0.469)
optimal_tokens = 0.143 * (budget_flops ** 0.531)
```
套用函数能得到:
如果预算:`1e21 FLOPs`(大约相当于几百万美元的 GPU 成本)
那么结论:
- 训练一个 **70B 参数**的模型(不是 700B,也不是 7B)
- 用 **2.4 万亿 tokens** 的数据(不是 1 万亿,也不是 10 万亿)
- 这个配比最优,既不浪费算力,loss 也最低
# Cues
[[科学计数法]]
# Notes
## Scaling Law 是什么,有几要素?
[[Scaling Law]]
## 一、模型、算力、数据、Loss四要素分别如何衡量
### 1. 模型参数如何衡量
可以看[[Transformer]]里的代码,如果FFN 里升维的时候是 4 倍升维,那么每个 Transformer Block是12 × d_model²的参数量
为啥是 4 倍:在标准 Transformer 中(如 GPT、BERT),通常采用:d_ff = 4 × d_model
```
每个 Block = 12 × d_model²
def forward(self, x):
x = x + self.attn(self.ln_1(x))
x = x + self.mlpf(self.ln_2(x))
return x
├── Attention: 4 × d_model²
│ ├── Q 投影矩阵: 1 × d_model²
│ ├── K 投影矩阵: 1 × d_model²
│ ├── V 投影矩阵: 1 × d_model²
│ └── 输出投影: 1 × d_model²
│
└── FFN: 8 × d_model²
├── c_fc (d_model → d_ff): 1 × (d_model × 4d_model) = 4 × d_model²
└── c_proj (d_ff → d_model): 1 × (4d_model × d_model) = 4 × d_model²
```
```
def get_num_parameters(self, d_model: int, num_layers: int) -> int:
"""Calculate number of non-embedding parameters."""
# Formula from assignment: 12 * num_layers * d_model^2
return 12 * num_layers * d_model * d_model
```
### 2. 数据如何衡量
[[token]]
T = train_steps × global_batch_size × seq_len
### 3. 计算资源(FLOPs)怎么算?
训练时的总计算量([[FLOPs]])约等于:`6 × 模型参数量 × 训练数据量 (tokens)`
为啥是 6 倍:
1. 前向传播:≈ 1N(每个参数参与一次矩阵运算)
2. 反向传播(激活梯度):≈ 2N(链式法则)
3. 反向传播(权重梯度):≈ 2N(计算每个权重的梯度)
4. 额外开销(激活函数、归一化等):≈ 1N
### 4. loss 怎么得到?
- 连接斯坦福的真实训练服务器
- 需要 API key 认证
- 有计算预算限制(budget_limit = 2e18)
- 训练脚本固化在远程服务器上了,`scaling_laws.py`只是调整[[超参数]]
- 服务器端实际训练模型并返回真实 loss
- 会消耗真实的计算资源
或者mock 数据 `demo_scaling_laws.py`
___
## 二、算力C不变, 找一组最优 N、D
"Iso" 的意思是“相等”。IsoFLOPs 就是在**计算量相等**的情况下,寻找最优的模型配置。
假设我们的固定预算是 **10,000 FLOPs**,可以有以下几种选择
- 改变模型参数:改变 d_model 与 num_layers(控制 P)。
- 改变数据规模:通过 train_steps 或子采样数据(控制 T)。
- 每次运行记录:P, T, C=6PT, 最终/末段均值的验证 loss(建议平滑最后若干 step 的 loss 抗噪)。
在一个固定的算力预算下,模型太大或太小都不好,存在一个最优的点。
```Java
Loss ^
5 | *
| / \
4 | / \* <-- 最优点
|
3 |
+-------------------> 参数量
(小) (中) (大)
```
| 参数量 (N) | | 能训练的数据量 (D) | 最终 Loss |
| :------ | :----- | :------------ | :------------ |
| 小模型 | 10 | 167 tokens | 5.2 |
| **中模型** | **20** | **83 tokens** | **4.8 ← 最优!** |
| 大模型 | 50 | 33 tokens | 5.5 |
对应的实验数据就像这样:
```json
[
{"parameters": 10, "compute_budget": 10000, "final_loss": 5.2},
{"parameters": 20, "compute_budget": 10000, "final_loss": 4.8},
{"parameters": 50, "compute_budget": 10000, "final_loss": 5.5}
]
```
通过在不同预算下重复上述实验,收集了一系列最优配置:
- 预算 **10k** FLOPs → 最优参数量 **20**
- 预算 **100k** FLOPs → 最优参数量 **200**
- 预算 **1M** FLOPs → 最优参数量 **2000**
[[幂律关系]]
发现了一个惊人的规律:**最优参数量 (N) 正比于计算预算 (C) 的某个幂次方**。画在对数坐标系上,它就是一条直线
```python
import numpy as np
budgets = np.array([10000, 100000, 1000000])
optimal_params = np.array([20, 200, 2000])
# 1. 对数变换,将幂律关系转换为线性关系
log_C = np.log(budgets) # [9.21, 11.51, 13.82]
log_N = np.log(optimal_params) # [3.00, 5.30, 7.60]
# 2. 线性拟合:log(N) = log(a) + b * log(C)
# 这不就是我们熟悉的 y = c + m*x 吗!
coeffs = np.polyfit(log_C, log_N, 1)
b = coeffs[0] # 斜率 (slope)
log_a = coeffs[1] # 截距 (intercept)
a = np.exp(log_a)
# 假设拟合结果是 b ≈ 0.5, a ≈ 0.22
# 我们的缩放定律就是:N ≈ 0.22 × C^0.5
```
## 三、算力改变,找到多组 N、D
最优参数量随着预算的增加而增加,在对数图上呈现线性关系。
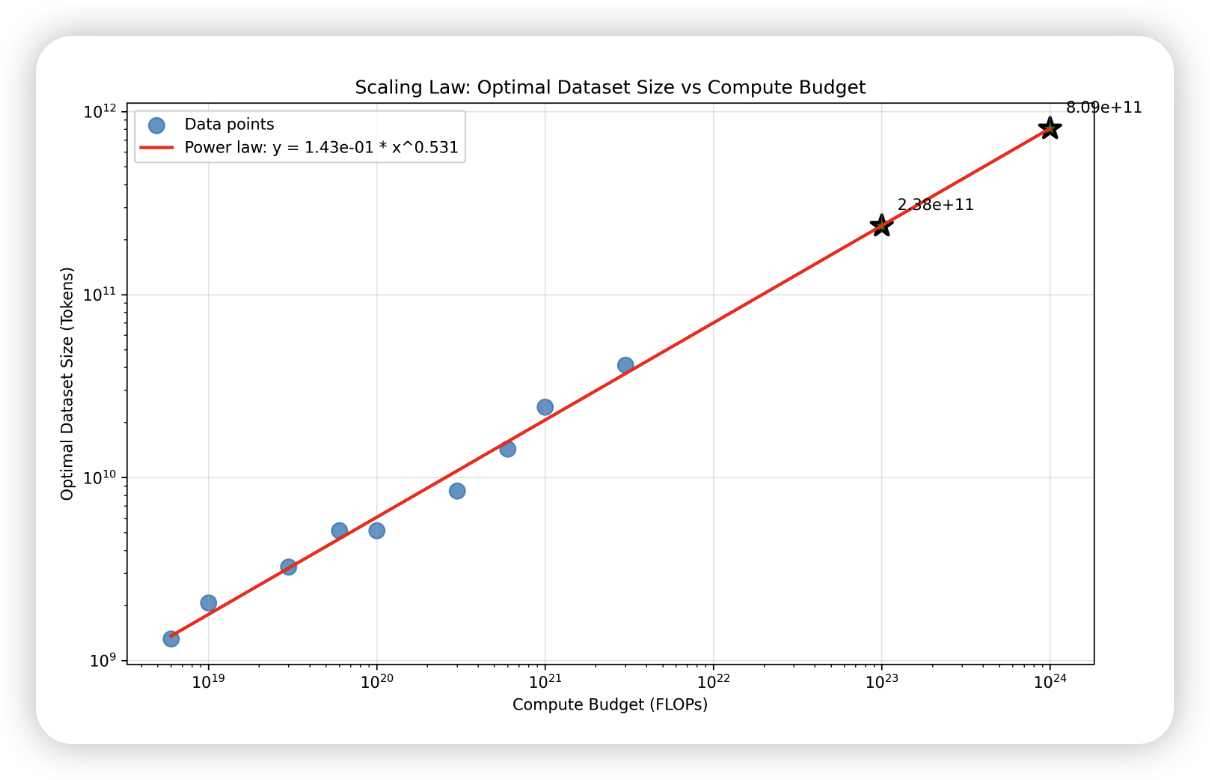
| Compute C (FLOPs) | Optimal N (params) | Optimal D (tokens) | Min Loss |
|:----------------- |:------------------ |:------------------ |:-------- |
| 6.00e+18 | 7.62e+08 | 1.31e+09 | 5.900 |
| 1.00e+19 | 8.07e+08 | 2.07e+09 | 5.618 |
| 3.00e+19 | 1.54e+09 | 3.25e+09 | 5.107 |
| 6.00e+19 | 1.95e+09 | 5.12e+09 | 4.831 |
| 1.00e+20 | 3.25e+09 | 5.12e+09 | 4.653 |
| 3.00e+20 | 5.90e+09 | 8.47e+09 | 4.311 |
| 6.00e+20 | 6.97e+09 | 1.43e+10 | 4.121 |
| 1.00e+21 | 6.86e+09 | 2.43e+10 | 4.003 |
| 3.00e+21 | 1.21e+10 | 4.12e+10 | 3.773 |
(对数-对数图)、[[幂律关系]]
```Java
log(N) ^
1e9 | * <-- 预测点
| *
1e6 | *
| *
1e3 | *
+-------------------> log(C:FLOPs)
1e15 1e17 1e19
```
函数的核心任务是拟合并输出三个关键的缩放定律:
1. **N(C)**: 模型大小 (Model Size) 与计算预算 (Compute Budget) 的关系。
2. **D(C)**: 数据集大小 (Dataset Size) 与计算预算的关系。
3. **L(C)**: 损失 (Loss) 与计算预算的关系。
- **Kaplan et al., 2020** “Scaling Laws for Neural Language Models” — 最早系统性给出三维幂律。([arXiv](https://arxiv.org/abs/2001.08361?utm_source=chatgpt.com "Scaling Laws for Neural Language Models"))
- **Bahri et al., 2021** “Explaining Neural Scaling Laws” — 从理论角度拆解 variance‑limited / resolution‑limited 两种 regime。([arXiv](https://arxiv.org/abs/2102.06701?utm_source=chatgpt.com "Explaining Neural Scaling Laws"))
- OpenAI blog“Training Compute‑Optimal GPT‑3” — 将公式落地到 GPU-hour 成本预估。
---
### 2. Kaplan vs Chinchilla 缩放定律
**Kaplan 定律(2020年)**:
- 建议:如果计算资源增加 10 倍,模型大小应该增加约 5.5 倍,数据只需增加 1.8 倍
- 比例:模型参数: 训练数据 ≈ 3:1
- 结果:导致了 GPT-3 这样的"大模型少数据"设计
**Chinchilla 定律(2022年)**:
- 发现:Kaplan 的结论有偏差!
- 建议:模型大小和数据量应该**同步增长**(1:1 比例)
- 核心发现:每个参数需要约 20 个 token 来训练才是最优的
举个例子:
- GPT-3:175B 参数,300B tokens(比例 1.7:1)- 严重欠训练!
- Chinchilla:70B 参数,1.4T tokens(比例 20:1)- 计算最优!