- [干了啥](#%E5%B9%B2%E4%BA%86%E5%95%A5) - [naive-softmax](#naive-softmax) - [[softmax](softmax.md)](#%5Bsoftmax%5D(softmax.md)) - [[[损失函数]]](#%5B%5B%E6%8D%9F%E5%A4%B1%E5%87%BD%E6%95%B0%5D%5D) - [将损失函数看作交叉熵](#%E5%B0%86%E6%8D%9F%E5%A4%B1%E5%87%BD%E6%95%B0%E7%9C%8B%E4%BD%9C%E4%BA%A4%E5%8F%89%E7%86%B5) - [negative sampling](#negative%20sampling) - [如果 K 等于 V-1 呢？](#%E5%A6%82%E6%9E%9C%20K%20%E7%AD%89%E4%BA%8E%20V-1%20%E5%91%A2%EF%BC%9F) - [数学知识点](#%E6%95%B0%E5%AD%A6%E7%9F%A5%E8%AF%86%E7%82%B9) # 干了啥 Word2vec 是一个软件包实际上包含：**两个算法**：continuous bag-of-words（CBOW）和 skip-gram。 - CBOW 是根据中心词周围的上下文单词来预测该词的词向量。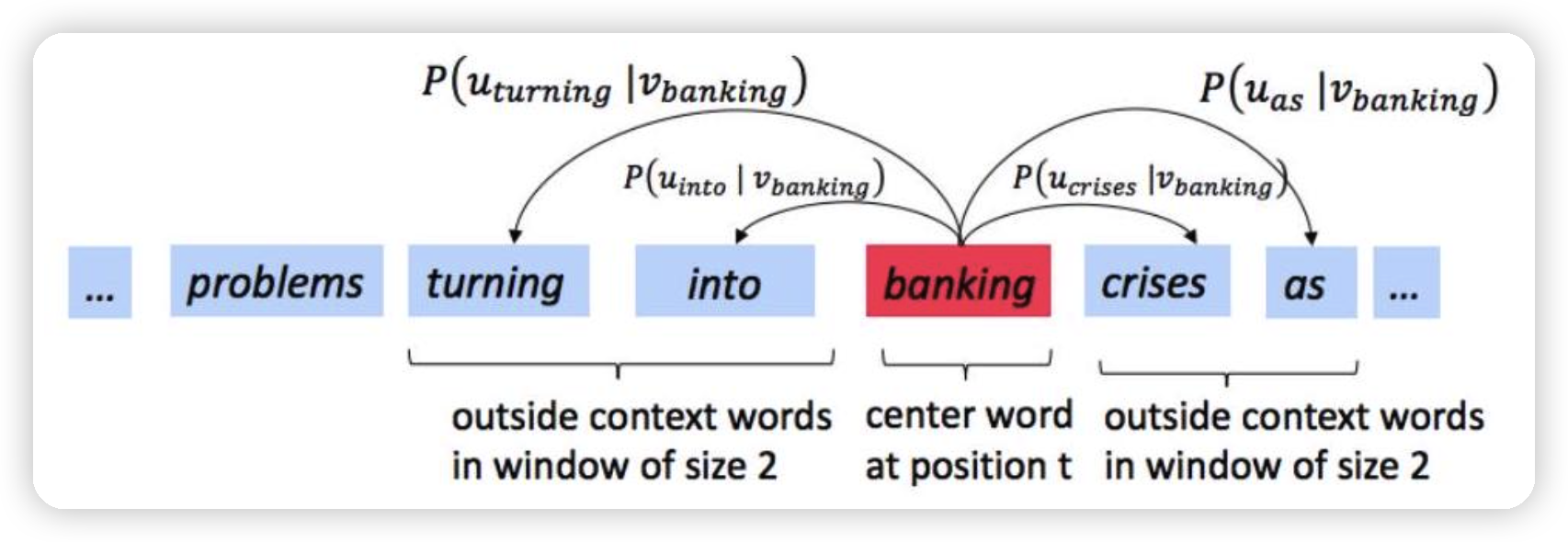 - skip-gram 则相反，是根据中心词预测周围上下文的词的概率分布。 在实现 skip-gram 的 word2vec 时，我们需要为每一个"中心词 (center word)"及其上下文"外词 (outside word)"计算损失并做梯度更新。**有两种主要方法**可以定义和计算这个损失： 1. **naive-softmax**：对整个词汇表做 softmax，计算开销与"词汇量"线性相关。 2. **negative sampling**：只对一个正样本 + K 个负样本做 sigmoid，计算开销与"K+1"线性相关，远小于词汇量。 在此 Lab 中会先介绍 naive-softmax（直观但计算量大），然后介绍 negative sampling（更高效），最后代码通常会使用 negative sampling，因为它在大词表时极大地减少了计算量。 # naive-softmax  $ P(O = o | C = c) = \frac{\exp(u_o^T v_c)}{\sum_{w \in \text{Vocab}} \exp(u_w^T v_c)} $ 在 Word2Vec 模型（特别是 Skip-gram 和 CBOW 模型）中用于计算 **给定中心词 (Context word) `c` 的情况下，生成目标词 (Output word) `o` 的概率** 的 Softmax 函数。 - **P(O = o | C = c)**: 在给定中心词 `c` 的条件下，目标词为 `o` 的概率。 - **o**: 目标词 (output word)。 - **c**: 中心词，也称为上下文词 (context word)。 - **Vocab**: 词汇表，即所有词的集合。 - **v\_c**: 中心词 `c` 的 **上下文词向量 (context word vector)**。在 Word2Vec 模型中，每个词都有两个向量表示：作为中心词的向量和作为目标词的向量。`v_c` 是当词 `c` 作为中心词时使用的向量。 - **u\_o**: 目标词 `o` 的 **目标词向量 (output word vector)**。`u_o` 是当词 `o` 作为目标词时使用的向量。 - **u\_o^T v\_c**: 向量 `u_o` 和 `v_c` 的 **点积 (dot product)**。点积衡量了两个向量的相似度。点积越大，向量越相似。 - **exp(x)**: 指数函数，`e` 的 `x` 次方。使用指数函数确保概率值始终为正数。 - **∑_{w ∈ Vocab} exp(u\_w^T v\_c)$**: **归一化项 (normalization term)**。分母是对所有词汇表 `Vocab` 中的词 `w`，计算 `exp(u_w^T v_c)` 并求和。这个求和过程确保了公式计算出的所有可能的输出词的概率总和为 1，符合概率的定义。 **实际例子** 为了简化，我们使用一个非常小的词汇表： **词汇表 Vocab = { "king", "queen", "man", "woman", "royal" }** 假设我们已经通过某种方式（比如训练 Word2Vec 模型）得到了每个词的向量表示。为了方便演示，我们假设这些向量是二维的，并且我们随意设定一些数值 (实际的词向量维度会更高，例如 100, 200, 300 维)： | 词语 | 目标词向量 u (作为输出词) | 上下文词向量 v (作为中心词) | |:------ |:----------------------- |:----------------------- | | king | `u_king` =[2, 1]| `v_king` =[2, 1]| | queen | `u_queen` =[2, 2]| `v_queen` =[2, 2]| | man | `u_man` =[1, 1]| `v_man` =[1, 1]| | woman | `u_woman` =[1, 2]| `v_woman` =[1, 2]| | royal | `u_royal` =[3, 3]| `v_royal` =[3, 3]| **例子计算：给定中心词 "king"，计算目标词为 "queen" 的概率 $P(O = "queen" | C = "king")$** 1. **计算点积 $u\_queen^T v\_king$**: - `u_queen` =[2, 2] - `v_king` =[2, 1] - `u_queen<sup>T</sup> v_king` = (2 \* 2) + (2 \* 1) = 4 + 2 = 6 2. **计算分子 exp(u\_queen^T v\_king)**: - `exp(6)` ≈ 403.43 3. **计算分母 ∑_{w ∈ Vocab} exp(u\_w^T v\_king)**: 我们需要计算词汇表中每个词 `w` 与中心词 "king" 的点积，并取指数，然后求和。 - `u_king<sup>T</sup> v_king` = (2 \* 2) + (1 \* 1) = 5 => `exp(5)` ≈ 148.41 - `u_queen<sup>T</sup> v_king` = 6 => `exp(6)` ≈ 403.43 (已计算过) - `u_man<sup>T</sup> v_king` = (1 \* 2) + (1 \* 1) = 3 => `exp(3)` ≈ 20.09 - `u_woman<sup>T</sup> v_king` = (1 \* 2) + (2 \* 1) = 4 => `exp(4)` ≈ 54.60 - `u_royal<sup>T</sup> v_king` = (3 \* 2) + (3 \* 1) = 9 => `exp(9)` ≈ 8103.08 分母 ∑_{w ∈ Vocab} exp(u\_w^T v\_king) ≈ 148.41 + 403.43 + 20.09 + 54.60 + 8103.08 ≈ 8729.61 4. **计算概率 P(O = "queen" | C = "king")**: - `P(O = "queen" | C = "king")` = `exp(u_queen<sup>T</sup> v_king)` / ∑_{w ∈ Vocab} exp(u\_w^T v\_king) - `P(O = "queen" | C = "king")` ≈ 403.43 / 8729.61 ≈ 0.046 **矩阵表示** 为了更好地理解公式，我们可以用矩阵来表示。 假设我们的词汇表大小为 V (这里 V=5)，词向量维度为 d (这里 d=2)。 1. **输出词向量矩阵 U (Output Word Vectors Matrix)**: 这是一个 V x d 的矩阵，每一行代表一个词作为 **目标词** 的向量表示。 ```Java U = | u_king^T | = | 2 1 | | u_queen^T | | 2 2 | | u_man^T | | 1 1 | | u_woman^T | | 1 2 | | u_royal^T | | 3 3 | ``` 2. **上下文词向量矩阵 V (Context Word Vectors Matrix)**: 这是一个 V x d 的矩阵，每一列代表一个词作为 **中心词** 的向量表示。为了方便矩阵乘法，我们通常使用 V^T，即转置后的矩阵，这样每一行代表一个词作为中心词的向量。 ```Java V^T = | v_king v_queen v_man v_woman v_royal | |-------------------------------------------------| | 2 2 1 1 3 | | 1 2 1 2 3 | ``` (注意，这里为了视觉上和U矩阵对应，我把 V^T 画成了每一行代表一个词，实际上在计算中，更常见的是 V 的每一列代表一个词，然后计算 U * V^T) 3. **计算所有可能的点积 (Conceptual Matrix Multiplication):** 虽然公式中我们是针对单个中心词 `c` 进行计算，但如果我们想一次性计算 **所有中心词作为输入，所有词作为输出** 的概率（概念上，实际训练中通常是 batch 计算），我们可以想象一个矩阵乘法的过程。 如果我们计算矩阵乘积 `U * V^T`，我们会得到一个 V x V 的矩阵，其中 **第 i 行第 j 列的元素 (i, j)** 就代表了 **u_{word\_i}^T v_{word\_j}** 的点积 (未取指数)。 ```Java U * V^T = | u_king^T | * | v_king v_queen v_man v_woman v_royal | | u_queen^T | |-------------------------------------------------| | u_man^T | | 2 2 1 1 3 | | u_woman^T | | 1 2 1 2 3 | | u_royal^T | = | u_king^T * v_king u_king^T * v_queen ... u_king^T * v_royal | | u_queen^T * v_king u_queen^T * v_queen ... u_queen^T * v_royal | | ... ... | | u_royal^T * v_king u_royal^T * v_queen ... u_royal^T * v_royal | = | 5 6 3 4 9 | (第一行，中心词 "king" 与所有词的点积) | 6 8 4 6 12 | (第二行，中心词 "queen" 与所有词的点积) | 3 4 2 3 6 | | 4 6 3 5 9 | | 9 12 6 9 18 | ``` ## [softmax](softmax.md) 1. **Softmax 应用 (按行进行 Softmax):** 为了得到概率 `P(O = o | C = c)`，我们需要对点积矩阵的 **每一行** 应用 Softmax 函数。例如，对于中心词 "king" (对应矩阵的第一行): - 我们对第一行的每个元素取指数：`[exp(5), exp(6), exp(3), exp(4), exp(9)]` ≈ `[148.41, 403.43, 20.09, 54.60, 8103.08]` - 然后，将每个指数值除以 **该行所有指数值的总和** (归一化)：分母 ≈ 8729.61 (我们在上面已经计算过)。 这样，矩阵的每一行都将转换为概率分布，**行索引代表中心词，列索引代表目标词，矩阵中的值代表给定中心词，目标词出现的概率**。 **总结** - 公式 `P(O = o | C = c) = \frac{\exp(u_o^T v_c)}{\sum_{w \in \text{Vocab}} \exp(u_w^T v_c)}` 使用 Softmax 函数将词向量的点积转换为概率。 - 矩阵 U 代表所有词作为目标词的向量，矩阵 V 代表所有词作为中心词的向量。 - 概念上，矩阵乘法 `U * V^T` 可以帮助我们理解如何一次性计算所有可能的词对之间的点积。 - Softmax 函数按行应用于点积矩阵，得到最终的概率矩阵。 ## [[损失函数]] 在 Word2Vec 中，我们的目标是最大化在给定中心词的情况下，观察到实际上下文词的概率。换句话说，我们希望模型预测的概率分布尽可能接近真实的概率分布。为了达到这个目标，我们需要定义一个损失函数来衡量模型预测与真实情况之间的差距。 对于单个词对 (c, o)，损失函数通常使用 **负对数似然 (Negative Log-Likelihood)**： $ J_{naive-softmax}(v_c, o, U) = - \log P(O = o | C = c) $ 这个公式的含义是： - **J_{naive-softmax}(v_c, o, U)**：损失函数，它依赖于中心词向量 v_c、目标词 o 和所有输出词向量的矩阵 U。 - **-log**：[[负对数]]。使用负对数的原因是： - 最大化概率 P(O = o | C = c) 等价于最小化其负对数 -log P(O = o | C = c)。 - 对数函数可以将连乘转换为连加，方便计算和优化。 - 对数函数在概率接近 0 时梯度变化较大，有助于模型更好地学习。 - **P(O = o | C = c)**：给定中心词 c，目标词为 o 的概率，就是你提供的 softmax 公式。 **结合你的例子解释损失函数** 我们继续使用你提供的例子： - **词汇表 Vocab = { "king", "queen", "man", "woman", "royal" }** - 以及你设定的词向量和计算出的概率：`P(O = "queen" | C = "king")` ≈ 0.046 现在，假设在我们的训练数据中，当中心词是 "king" 时，实际的上下文词（也就是我们希望模型预测的词）确实是 "queen"。这意味着对于这个特定的词对 ("king", "queen")，我们希望 `P(O = "queen" | C = "king")` 尽可能接近 1。 使用损失函数计算： $ J_{naive-softmax}(v_{king}, "queen", U) = - \log P(O = "queen" | C = "king") $ $ J_{naive-softmax}(v_{king}, "queen", U) = - \log (0.046) $ $ J_{naive-softmax}(v_{king}, "queen", U) ≈ 3.08 $ 这个 3.08 就是这个词对 ("king", "queen") 的损失值。 **损失值的意义**  - **损失值越大，表示模型预测得越差。** 例如，如果模型预测 `P(O = "queen" | C = "king")` 非常小（比如 0.001），那么损失值就会非常大（-log(0.001) ≈ 6.91）。 - **损失值越小，表示模型预测得越好。** 如果模型预测 `P(O = "queen" | C = "king")` 非常接近 1（比如 0.9），那么损失值就会非常小（-log(0.9) ≈ 0.11）。 **训练过程** 在 Word2Vec 的训练过程中，我们会遍历大量的词对 (c, o)，并计算每个词对的损失值。然后，使用优化算法（例如梯度下降）来调整词向量 (u_w 和 v_w)，使得所有词对的平均损失值尽可能小。通过不断地调整词向量，模型最终能够学习到词语之间的语义关系。 **总结** 损失函数 `-log P(O = o | C = c)` 的作用是衡量模型预测的概率与真实概率之间的差距。通过最小化损失函数，我们可以训练 Word2Vec 模型，使其能够更好地预测给定中心词的上下文词。你提供的例子很好地说明了如何使用 softmax 公式计算概率，而损失函数则是在此基础上衡量模型预测的质量。 这段话解释了 Word2Vec 中使用的损失函数（通常是负对数似然）可以被视为真实分布和预测分布之间的交叉熵。下面我来详细解释这段话的含义，并结合前面的例子进行说明。 ## 将损失函数看作交叉熵 这段话的核心思想是将 Word2Vec 的损失函数与交叉熵联系起来。交叉熵是信息论中一个重要的概念，用于衡量两个概率分布之间的差异。 **关键概念** 1. **真实分布 y：** 在 Word2Vec 中，真实分布 y 是一个 one-hot 向量。这意味着： - 对于给定的中心词 c，只有一个词是真正的上下文词 o。 - 在 y 向量中，对应于真实上下文词 o 的位置上的值为 1，其他位置上的值都为 0。 例如，如果中心词是 "king"，真实的上下文词是 "queen"，而词汇表是 { "king", "queen", "man", "woman", "royal" }，那么 y 向量就是[0, 1, 0, 0, 0]。 2. **预测分布 ŷ：** 预测分布 ŷ 是模型根据中心词 c 预测出的上下文词的概率分布。 - ŷ 向量中的每个元素表示模型预测某个词作为上下文词的概率。 - ŷ 向量是通过 softmax 函数计算得到的，即 P(O | C = c)。 例如，根据前面的例子，我们计算出 `P(O = "queen" | C = "king")` ≈ 0.046。假设模型预测出的完整概率分布是 ŷ =[0.1, 0.046, 0.2, 0.3, 0.354]，分别对应 "king", "queen", "man", "woman", "royal" 的概率。 3. **交叉熵：** 交叉熵用于衡量两个概率分布之间的差异。对于离散概率分布，交叉熵的计算公式如下： H(y, ŷ) = - Σ_i y_i log(ŷ_i) 其中，y_i 和 ŷ_i 分别表示在第 i 个事件上的真实概率和预测概率。 **将交叉熵应用于 Word2Vec** 在 Word2Vec 中，我们将交叉熵应用于真实分布 y 和预测分布 ŷ。由于 y 是一个 one-hot 向量，所以交叉熵的计算可以简化为： H(y, ŷ) = - log(ŷ_o) 其中，ŷ_o 是预测分布 ŷ 中对应于真实上下文词 o 的概率值。 这正好就是我们之前提到的负对数似然损失函数！ **例子说明** 继续使用之前的例子： - 中心词 c = "king" - 真实上下文词 o = "queen" - 真实分布 y =[0, 1, 0, 0, 0] - 预测分布 ŷ =[0.1, 0.046, 0.2, 0.3, 0.354] 计算交叉熵： H(y, ŷ) = - (0 * log(0.1) + 1 * log(0.046) + 0 * log(0.2) + 0 * log(0.3) + 0 * log(0.354)) H(y, ŷ) = - log(0.046) ≈ 3.08 这与我们之前计算的负对数似然损失值完全一致。 **这段话的意义** 这段话说明了 Word2Vec 的损失函数可以从信息论的角度进行解释，即通过最小化预测分布和真实分布之间的交叉熵来训练模型。这种解释更加深刻地揭示了 Word2Vec 的工作原理：模型的目标是学习一个概率分布，使其尽可能接近真实的上下文分布。 **总结** 这段话将 Word2Vec 的损失函数与交叉熵联系起来，提供了一个更广阔的视角来理解 Word2Vec 的训练过程。通过最小化交叉熵，模型能够学习到词语之间的语义关系，并能够根据中心词有效地预测上下文词。希望以上解释能够帮助你理解这段话的含义。 # negative sampling **回顾之前的例子** - **词汇表 Vocab = { "king", "queen", "man", "woman", "royal" }** - 我们计算了 `P(O = "queen" | C = "king")` ≈ 0.046，使用了 naive softmax。 - 我们也计算了使用负对数似然的损失函数：`J<sub>naive-softmax</sub>(v<sub>king</sub>, "queen", U)` ≈ 3.08 **Negative Sampling 的核心思想** Negative sampling 的核心思想是：与其计算整个词汇表的 softmax（计算量巨大），不如只关注 **一个正样本** 和 **几个负样本**。 - **正样本 (Positive Sample):** 实际出现在中心词上下文中的词。在我们的例子中，("king", "queen") 是一个正样本。 - **负样本 (Negative Sample):** 没有出现在中心词上下文中的词。我们需要随机抽取一些词作为负样本。 **Negative Sampling 的步骤** 1. **选择正样本：** 假设我们的训练数据中有一个词对 ("king", "queen")。 2. **选择负样本：** 我们需要从词汇表中随机选择 K 个词作为负样本。K 是一个超参数，通常取 5-20。为了简化，我们假设 K=2，并且我们随机选择了 "man" 和 "royal" 作为负样本。 3. **构建数据集：** 我们现在有了一个新的数据集，包含一个正样本和两个负样本： ```Java | 中心词 (c) | 目标词 (o) | 标签 (Label) | |:--------- |:--------- |:----------- | | "king"    | "queen"   | 1          | | "king"    | "man"     | 0          | | "king"    | "royal"   | 0          | 标签 1 表示正样本，标签 0 表示负样本。 ``` 1. **使用 Sigmoid 函数：** 对于每个样本，我们使用 sigmoid 函数来预测目标词是否是中心词的上下文： $ P(O = o | C = c) = \sigma(u_o^T v_c) = \frac{1}{1 + \exp(-u_o^T v_c)} $ 其中 σ 是 sigmoid 函数。 1. **定义损失函数：** 对于 negative sampling，损失函数定义为：正样本的损失+负样本的损失 $ J_{neg-sample}(v_c, o, U) = -\log(\sigma(u_o^T v_c)) - \sum_{k=1}^K \log(\sigma(-u_k^T v_c)) $ σ（小写希腊字母 sigma）通常用来表示 sigmoid 函数。 对于正样本，我们希望模型预测其为正样本的概率尽可能高。而要使 $\sigma(u_o^T v_c)$ 接近 1，我们需要使 ​$u_o^T v_c$ 尽可能大（[Sigmoid函数](Sigmoid函数.md)图像） 所以： - 第一项是正样本的损失。我们希望 σ(uoT​vc​) 尽可能接近 1（此时负指数为 0）。    - 第二项是 K 个负样本的损失。我们希望$\log(\sigma(-u_k^T v_c))$尽可能接近 0，也就是 $\sigma(-u_k^T v_c)$ 尽可能接近 1，因为 $σ(−x)=1−σ(x)$，所以也就是 $\sigma(u_o^T v_c)$ 尽可能接近 0。 **例子计算** 我们来计算上面例子中三个样本的损失： 1. **正样本 ("king", "queen", 1):** - `u_queen^T v_king` = 6 (之前计算过)     - `σ(6)` ≈ 0.9975     - −log(σ(6)) ≈ -log(0.9975) ≈ 0.0025 1. **负样本 ("king", "man", 0):** - `u_man^T v_king` = 3 (之前计算过)     - `σ(-3)` ≈ 0.0474     - −log(σ(−3)) ≈ -log(0.0474) ≈ 3.047 1. **负样本 ("king", "royal", 0):** - `u_royal^T v_king` = 9 (之前计算过)     - `σ(-9)` ≈ 0.000123     - −log(σ(−9)) ≈ -log(0.000123) ≈ 8.91 **总损失** 对于这个中心词 "king"，总的 negative sampling 损失是这三个样本损失的总和： 总损失 ≈ 0.0025 + 3.047 + 8.91 ≈ 11.96 **与 Naive Softmax 的比较** - **计算量：** Naive softmax 需要计算整个词汇表的 softmax，计算量与词汇表大小 V 成正比。而 negative sampling 只需计算 K+1 个 sigmoid 函数，计算量与 K 成正比，通常 K 远小于 V，因此计算效率大大提高。 - **损失函数：** Naive softmax 使用负对数似然和 softmax 函数，而 negative sampling 使用 sigmoid 函数和略有不同的损失函数。 **总结** Negative sampling 通过只关注少量正负样本，大大降低了 Word2Vec 的计算复杂度，使其能够在大规模语料库上进行训练。它使用 sigmoid 函数将问题转化为二分类问题，并使用相应的损失函数进行优化。希望这个结合你之前例子的讲解能够帮助你更好地理解 negative sampling。 # 如果 K 等于 V-1 呢？ 你提出了一个很好的问题：如果负采样中的 K（负样本的数量）等于 V-1（词汇表大小减 1），会发生什么？在这种情况下，负采样的计算量还会比朴素 softmax 小吗？ **分析** - **朴素 softmax：** 计算复杂度是 O(V)，其中 V 是词汇表的大小。这意味着计算量与词汇表大小成正比。 - **负采样：** 计算复杂度是 O(K+1)，其中 K 是负样本的数量。在这种情况下，K = V-1，所以计算复杂度变成了 O(V)。 因此，当 K = V-1 时，负采样的计算复杂度与朴素 softmax *相同*，都是 O(V)。 **为什么通常 K 远小于 V？** 负采样的主要目的是为了解决朴素 softmax 在大规模词汇表上的计算瓶颈。在实际应用中，词汇表通常非常大（例如，几万到几十万甚至更大），而负样本的数量 K 通常设置得比较小（例如，5 到 20）。 - **计算效率：** 通过使 K 远小于 V，负采样的计算量可以显著降低，从而提高训练速度。 - **经验结果：** 经验表明，使用相对较小的 K 值也能取得良好的训练效果。 **K = V-1 的情况实际上退化成了什么？** 当 K = V-1 时，我们实际上是在对除了正样本之外的所有词都进行了负采样。这意味着对于每个中心词，我们都在考虑它与词汇表中所有其他词的关系。这在某种程度上类似于朴素 softmax 的思想，即考虑所有可能的输出词。 然而，即使在这种情况下，负采样仍然与朴素 softmax 有一些关键区别： 1. **损失函数不同：** 负采样使用 sigmoid 函数进行二分类，而朴素 softmax 使用 softmax 函数进行多分类。这意味着它们的优化目标和梯度计算方式是不同的。 2. **计算方式不同：** 即使计算量相同，负采样在实现上也是分别计算每个正负样本的损失，然后求和。而朴素 softmax 需要一次性计算整个词汇表的概率分布。这在内存使用和并行计算方面可能存在差异。 **总结** 当 K = V-1 时，负采样的计算复杂度与朴素 softmax 相同，都是 O(V)。但负采样的主要优势在于当 K 远小于 V 时，可以显著降低计算量，提高训练效率。在实际应用中，通常会选择较小的 K 值，以达到效率和效果的平衡。即使 K=V-1，负采样在损失函数和计算方式上仍然与朴素 softmax 有区别。 因此，虽然理论上 K 可以等于 V-1，但在实践中，这样做既没有必要，也失去了负采样方法的核心优势。通常情况下，选择远小于 V 的 K 值是更明智的选择。 # 数学知识点 1. 概率论相关： - 条件概率 (Conditional Probability) - 概率分布 (Probability Distribution) - 经验分布 (Empirical Distribution) - [[最大似然估计]] 1. 线性代数相关： - 向量 (Vectors) - 矩阵 (Matrices) - 点积/内积 (Dot Product) - 转置 (Transpose，出现在 u^T v 形式) 1. 微积分相关： - [[偏导数]] (Partial Derivatives) - [[梯度]] (Gradients) - [Sigmoid函数](Sigmoid函数.md)及其导数 - 链式法则 (Chain Rule，在求导过程中隐含使用) 1. 其他数学概念： - [[softmax]] - [[交叉熵 cross_entropy]] (Cross Entropy) - 对数函数 (Logarithm，出现在损失函数中) - one-hot 向量 - 指数函数 (Exponential Function，在 softmax 和 sigmoid 中) 1. 优化相关： - 损失函数 (Loss Function) - 负采样 (Negative Sampling) - 最小化问题 (Minimization) # 代码 **2. (a) (12 分) word2vec.py - 词向量模型组件实现** 此部分的目标是在 word2vec.py 文件中实现 word2vec 模型的核心组成部分，包括 sigmoid 函数、基于朴素 Softmax 的损失函数和梯度计算、基于负采样的损失函数和梯度计算，以及 Skip-gram 模型。 - **sigmoid(x) 函数** - **功能:** 实现 Sigmoid 函数，其数学表达式为 σ(x) = 1 / (1 + e^(-x))。该函数将任意实数输入映射到 (0, 1) 区间，常用于将线性输出转换为概率值。 - **实现要求:** 编写 Python 函数 sigmoid(x)，接受一个数值或 NumPy 数组作为输入 x，并返回应用 Sigmoid 函数后的结果。需使用 NumPy 库以保证效率。 - **naiveSoftmaxLossAndGradient(centerWordVec, outsideWordIdx, outsideVectors, dataset) 函数** - **功能:** 实现基于朴素 Softmax 的损失函数及其梯度计算。该函数用于计算给定中心词向量 centerWordVec 和目标外部词索引 outsideWordIdx 时的 Softmax 损失，并计算损失函数关于中心词向量和所有外部词向量的梯度。 - **原理:** 朴素 Softmax 损失旨在最大化目标外部词在给定中心词条件下的条件概率 P(O=o|C=c)。损失函数通常定义为负对数似然，即 J_naive-softmax(vc, o, U) = -log P(O=o|C=c)。梯度计算需要根据链式法则，分别计算损失函数对中心词向量 vc 和外部词向量矩阵 U 的偏导数。 - **计算复杂度:** 朴素 Softmax 的计算复杂度与词汇表大小成正比，因此对于大型词汇表，计算成本较高。 - **实现要求:** 编写 Python 函数 naiveSoftmaxLossAndGradient，输入包括中心词向量、外部词索引、外部词向量矩阵和数据集对象。函数应返回损失值、中心词向量的梯度 gradCenterVec 以及外部词向量矩阵的梯度 gradOutsideVecs。需使用 NumPy 库进行高效的矩阵和向量运算，并参考书面部分的公式进行梯度推导和实现。 - **negSamplingLossAndGradient(centerWordVec, outsideWordIdx, outsideVectors, dataset, k=10) 函数** - **功能:** 实现基于负采样的损失函数及其梯度计算。负采样是一种近似 Softmax 的方法，旨在提高训练效率。该函数计算给定中心词向量 centerWordVec 和目标外部词索引 outsideWordIdx，以及 k 个负样本时的负采样损失，并计算损失函数关于中心词向量、目标外部词向量和负样本词向量的梯度。 - **原理:** 负采样损失函数旨在区分真实的正样本（中心词-外部词对）和随机抽取的负样本。损失函数由两部分组成：一部分最大化正样本的 Sigmoid 输出，另一部分最小化负样本的 Sigmoid 输出。损失函数形式为 J_neg-sample(vc, o, U) = -log(σ(uo^T vc)) - Σ_{k=1}^K log(σ(-uk^T vc))。梯度计算需分别针对中心词向量、目标外部词向量和每个负样本词向量进行。 - **计算效率:** 负采样显著降低了计算复杂度，使其适用于大型词汇表的训练。 - **实现要求:** 编写 Python 函数 negSamplingLossAndGradient，输入包括中心词向量、外部词索引、外部词向量矩阵、数据集对象和负样本数量 k。函数应返回损失值、中心词向量的梯度 gradCenterVec、目标外部词向量的梯度 gradOutsideVecs 以及负样本词向量的梯度 (可以累加到 gradOutsideVecs 中)。需使用 NumPy 和 Sigmoid 函数的导数进行计算，并参考书面部分的公式。数据集对象可能提供负样本抽样的方法。 - **skipgram(centerWordIdx, outsideWordIdxs, centerWordVectors, outsideVectors, dataset, lossType='naive') 函数** - **功能:** 实现 Skip-gram 模型的前向传播和梯度计算。该函数针对给定的中心词索引 centerWordIdx 和一组外部词索引 outsideWordIdxs，使用指定的损失函数类型 (lossType) 计算总损失和梯度。 - **原理:** Skip-gram 模型的目标是根据中心词预测其上下文词。对于一个中心词及其上下文窗口，模型需要遍历窗口内的每个外部词，计算损失并累积梯度。损失函数类型可以是 'naive' (朴素 Softmax) 或 'negSample' (负采样)。总损失是窗口内所有中心词-外部词对损失之和。梯度也需要对窗口内所有词对的梯度进行累加。 - **实现要求:** 编写 Python 函数 skipgram，输入包括中心词索引、外部词索引列表、中心词向量矩阵、外部词向量矩阵、数据集对象和损失函数类型。函数应根据 lossType 调用相应的损失函数和梯度计算函数 (naiveSoftmaxLossAndGradient 或 negSamplingLossAndGradient)，遍历 outsideWordIdxs 中的每个外部词索引，累加损失和梯度。最终返回总损失 totalLoss，中心词向量矩阵的梯度 gradCenterVecs 和外部词向量矩阵的度 gradOutsideVecs。 **测试 word2vec.py:** 完成上述函数实现后，运行 python word2vec.py 脚本进行单元测试，验证各函数的实现是否符合预期。 **2. (b) (4 分) sgd.py - 随机梯度下降优化器实现** - **sgd(initialParameters, gradientFunction, step, batchSize, alpha=0.01) 函数** - **功能:** 实现随机梯度下降 (SGD) 优化算法。该函数接收初始模型参数 initialParameters、梯度计算函数 gradientFunction、当前迭代步数 step、批量大小 batchSize 和学习率 alpha。函数执行一次 SGD 更新，根据梯度更新模型参数，并返回更新后的参数和损失值。 - **原理:** SGD 是一种迭代优化算法，用于最小化损失函数。每次迭代，SGD 使用梯度计算函数 gradientFunction 计算当前参数下的损失和梯度，然后根据学习率 alpha 和梯度方向更新参数：parameters = parameters - alpha * gradients。 - **实现要求:** 编写 Python 函数 sgd，输入包括初始参数、梯度函数、迭代步数、批量大小和学习率。函数应调用 gradientFunction 获取损失和梯度，并根据 SGD 更新规则更新 initialParameters。返回更新后的参数 updatedParameters 和损失值 loss。 **测试 sgd.py:** 运行 python sgd.py 脚本进行单元测试，验证 SGD 优化器的实现是否正确。 **2. (c) (4 分) run.py - 模型训练与可视化** - **get_datasets.sh 脚本:** 运行 sh get_datasets.sh 下载 Stanford Sentiment Treebank (SST) 数据集，该数据集用于训练词向量。 - **run.py 脚本:** 运行 python run.py 执行以下步骤： 1. **数据加载:** 加载 SST 数据集。 2. **参数初始化:** 随机初始化中心词向量矩阵和外部词向量矩阵。 3. **训练循环:** 进行指定迭代次数 (例如 40,000 次) 的 SGD 训练。在每次迭代中： - 从数据集中随机选择一个语境窗口。 - 调用 skipgram 函数计算损失和梯度。 - 调用 sgd 函数更新词向量参数。 4. **可视化:** 使用 t-SNE 降维算法将高维词向量降至二维，并绘制散点图，保存为 word_vectors.png 文件。可视化目的是为了直观地观察学习到的词向量空间，例如语义相似的词是否在图中距离较近。 - **分析 word_vectors.png:** 训练完成后，分析生成的 word_vectors.png 图像。观察图中词向量的分布，例如是否存在语义相关的词簇，并对观察结果进行简要描述。 此部分无需编写代码，只需运行脚本并分析结果。重点在于理解训练流程和分析可视化结果。